Kurs:Statistik für Anwender/Exponentialverteilte Zufallsvariablen

Exponentialverteilte ZV

Definition exponentialverteilte ZV

Sei $\lambda >0$ gegeben.

Eine ZV $X$ mit der W-Dichte $f:ℝ\to [0,\mathrm{\infty }),f(t)=\{\begin{array}{ccc}\lambda \cdot e^{-\lambda t}& ,& \text{falls}t\ge 0\\ 0& ,& \text{sonst}\end{array}$
heißt exponentialverteilt zum Parameter $\lambda$.

Verteilungsfunktion exponentialverteilte ZV

Für die Verteilungsfunktion $F$ von $X$ gilt dann: $$F(x)=\underset{-\mathrm{\infty }}{\overset{x}{\int }}f(t)dt=\{\begin{array}{ccc}0& ,& \text{falls}x\in ]-\mathrm{\infty },0]\\ 1-e^{-\lambda x}& ,& \text{falls}x\in [0,\mathrm{\infty }[\end{array}$$

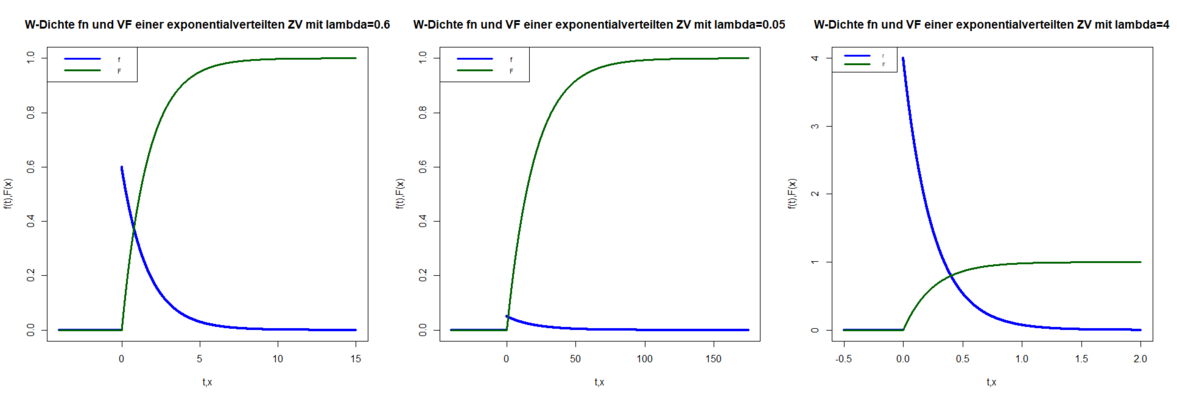
Beispiel exponentialverteilte ZV

Beispiel exponentialverteilte ZV interaktiv

Interaktive Shiny-App zur Exponentialverteilung:
Download und Link

Wahrscheinlichkeiten exponentialverteilte ZV

Für eine zum Parameter $\lambda$ exponentialverteilte ZV $X$ gilt: $P(0\le X)=1$
Weiterhin gilt für beliebige Zahlen $u,v$ mit $0\le u\le v$: $$P(X\le v)=1-\exp (-\lambda v),P(u\le X)=\exp (-\lambda u),$$ $$P(u\le X\le v)=\exp (-\lambda u)-\exp (-\lambda v)$$

Erwartungswert und Varianz exponentialverteilte ZV

Für eine zum Parameter $\lambda$ exponentialverteilte ZV $X$ gilt: $$E(X)=\frac{1}{\lambda }\text{und}V(X)=\frac{1}{{\lambda }^2}$$

Praktische Anwendung exponentialverteilte ZV

Exponentialverteilte ZV sind als Modell geeignet, wenn eine ZV $X$ die Wartezeit auf ein bestimmtes Ereignis beschreibt, und man annimmt, dass sich die Wahrscheinlichkeit für das Eintreten des Ereignis in einem festgelegten (zukünftigen) Zeitraum nicht ändert, wenn das Ereignis eine Zeitlang nicht eingetreten ist.
Genauer: Für exponentialverteilte ZV gilt: $P(0\le X\le {\delta }_t)=P(t_0\le X\le t+{\delta }_t|t_0\le X)$ (für $t,{\delta }_t\ge 0$)
Der Parameter $\lambda$ gibt dabei die Häufigkeitsrate (in der Einheit $\frac{1}{\text{ Zeiteinheit}}$) an, mit der das Ereignis eintritt, man nennt $\lambda$ zum Beispiel Ausfallrate, wenn das betreffende Ereignis, der Ausfall eines Objekts ist.

Beispiel Anwendung exponentialverteilte ZV

• ’Lebensdauer’ von Bauteilen, wenn Alterungserscheinungen nicht betrachtet werden

• Lebensdauer von Tieren, wenn Alterungserscheinungen vernachlässigt werden

• ’Lebensdauer’ von Atomen bei radioaktiven Zerfall

• Zeitspanne zwischen zwei Verkehrsunfällen (an einem bestimmten Ort)

Beispiel I

Für eine zum Parameter $\lambda =3$ exponentialverteilte ZV $Z$ gilt:
$$P(Z\le 0.4)=0.6988,$$
$$P(Z\ge 0.1)=0.74$$
Außerdem ist $E(Z)=0.3333$ und ${\sigma }_Z=0.3333$.

Beispiel II

Für eine zum Parameter $\lambda =0.00002$ exponentialverteilte ZV $Z$ gilt:
$$\begin{array}{cc}P(30000\le Z\le 50000)& =0.1809\end{array}$$
Außerdem ist $E(Z)=50000$ und ${\sigma }_Z=50000$.

Exponentialverteilte ZV in R

Für eine zum Parameter $\lambda$ exponentialverteilte ZV $X$ berechnet man in R:

• die Funktionswerte der W-Dichte von $X$ durch: $f(t)=dexp(t,\lambda )$
• die Funktionswerte der VF von $X$ durch: $F(x)=pexp(x,\lambda )$
• die Wahrscheinlichkeit für $X\in [u,v]$ durch: $P(u\le X\le v)=pexp(v,\lambda )-pexp(u,\lambda )$

Aufgabe

Sie betreiben eine Wildtierkamera und Sie wissen, dass die Wartezeit

$W$

, bis die Kamera ein Foto macht, als exponentialverteilt angenommen werden kann und die durchschnittliche Wartezeit

$E(W)=10$

Stunden beträgt.

1. Wie groß ist die Standardabweichung der Wartezeit?
2. Mit welcher Wahrscheinlichkeit warten Sie höchstens / mindestens $10$ Stunden ?
3. Mit welcher Wahrscheinlichkeit warten Sie exakt $13$ Stunden und $4.8$ Minuten?
4. Mit welcher Wahrscheinlichkeit warten Sie zwischen $11$ und $17$ Stunden?

Punktschätzung für den Parameter

Sei $X$ eine exponentialverteilte ZV, für die der Parameter $\lambda >0$ unbekannt ist.
Basierend auf einer Stichprobe $x_1,\dots ,x_n$ ist folgende Punktschätzung sinnvoll:

• $\lambda$ wird geschätzt durch: $\hat{\lambda }=\frac{1}{\bar{x}}=\frac{n}{\sum _{j=1}^n{x}_j}$

Intervallschätzung für den Parameter

Sei $X$ eine exponentialverteilte ZV, für die $\lambda >0$ unbekannt ist.

Bestimmung des arithmetischen Mittels

Basierend auf einer Stichprobe $x_1,\dots ,x_n$ berechnet man zunächst
$$\bar{x}=\frac{1}{n}\cdot \sum _{j=1}^n{x}_j$$

Bestimmung der Intervallgrenzen

Daraus ausgehend kann man nun wie folgt eine Intervallschätzung für $\lambda$ zu einem vorgegebenen Konfidenzniveau $\delta \stackrel{\text{z.B.}}{=}0.95$ berechnen:

Sind $q_U(=q_{[{\chi }^2,2n,\frac{1-\delta }{2}]})\in ]0,\mathrm{\infty }[$ und $q_O(=q_{[{\chi }^2,2n,\frac{1+\delta }{2}]})\in ]0,\mathrm{\infty }[$ die Zahlen mit
$$S_{2n}(q_U)=\frac{1-\delta }{2}\text{und}{S}_{2n}(q_O)=\frac{1+\delta }{2},$$
so erhält man eine Intervallschätzung $[{\lambda }_U,{\lambda }_O]$ für $\lambda$ durch: $$[{\lambda }_U,{\lambda }_O]=[\frac{q_U}{2n\bar{x}},\frac{q_O}{2n\bar{x}}]$$

Konfidenzniveau

Es ist bewiesen, dass diese Methode zur Berechnung einer Intervallschätzung für $\lambda$ das vorgegebene Konfidenzniveau $\delta$ einhält, das heißt unabhängig vom wahren Wert von $\lambda$ ist vor der Erhebung der Daten garantiert:
$$P(\lambda \in [{\lambda }_U,{\lambda }_O])\ge \delta$$

Anmerkungen

• Hier gilt sogar: $P(\lambda \in [{\lambda }_U,{\lambda }_O])=\delta$
• Man beachte, dass dabei die Intervallgrenzen ${\lambda }_U$ und ${\lambda }_O$ bzw. vom Zufall abhängen (denn für ihre Berechnung werden die Daten $x_1,\dots ,x_n$ verwendet). Andererseits ist $\lambda$ zwar unbekannt, aber fest und hängt daher nicht vom Zufall ab. Nachdem man das Konfidenzintervall berechnet hat, ist die Aussage $\lambda \in [{\lambda }_U,{\lambda }_O]$ daher entweder wahr oder falsch, man kann ihr aber keine Wahrscheinlichkeit mehr zuweisen.

Beispiel 1.1

An einem Verkehrsknotenpunkt passieren viele Unfälle. Die ZV $X$ beschreibt die Zeit (in Tagen), die dort zwischen zwei Unfällen liegt. Da man davon ausgehen kann, dass zukünftige Unfälle weder wahrscheinlicher noch unwahrscheinlicher werden, wenn eine Zeitlang kein Unfall passiert ist, kann man $X$ als exponentialverteilt annehmen. Es wird eine Stichprobe für $X$ der Länge $n=60$ erhoben, dabei erhält man die folgenden Daten: $$\begin{array}{c}1.20,2.47,9.35,4.36,25.55,5.12,6.51,0.31,17.44,0.89,2.30,8.78,4.16,4.27,23.20,\\ 4.03,7.75,0.77,0.27,7.31,3.33,12.99,3.36,5.40,3.56,37.94,0.50,1.92,14.93,6.70,\\ 9.32,1.53,14.04,0.60,2.88,2.03,7.58,24.88,0.54,19.13,0.62,16.76,10.09,17.10,1.57,\\ 2.57,0.16,10.36,9.29,2.43,2.86,25.04,3.31,4.49,4.45,23.65,6.16,12.74,0.13,18.15\end{array}$$

Beispiel 1.2

Daraus berechnet man: $\bar{X}=8.0188$
Wir berechnen nun eine Intervallschätzung für $\lambda$ zum Konfidenzniveau $\delta =0.9$:
Daraus berechnet man nun:
$$[{\lambda }_U,{\lambda }_O]=[0.0994,0.1523]$$

Aufgabe 1.1

An einer Kreuzung wird mehrfach die Zeit zwischen zwei Unfällen festgestellt. Es ergeben sich die folgenden Daten (gemessen in Tagen): $$12,2,62,31,89,6,32,12,5,177.$$
Wir nehmen an, dass die Zeitspanne zwischen zwei Unfällen durch eine exponentialverteilte ZV $X$ mit unbekanntem Parameter $\lambda$ beschrieben werden kann.

1. Berechnen Sie eine Punktschätzung für $\lambda$. Angenommen, die eben berechnete Punktschätzung entspricht dem wahren Wert von $\lambda$. Wie groß ist dann die Wahrscheinlichkeit, dass der nächste Unfall innerhalb von 10 Tagen passiert?

Aufgabe 1.2

2. Berechnen Sie eine Intervallschätzung für den unbekannten Parameter $\lambda$ der Exponentialverteilung zum Konfidenzniveau $\delta =0.8$. Angenommen, diese Intervallschätzung ist korrekt. Innerhalb welcher Grenzen liegt dann die Wahrscheinlichkeit dafür, dass der nächste Unfall innerhalb von 10 Tagen passiert.

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Exponentialverteilte%20Zufallsvariablen
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.