Kurs:Statistik für Anwender/Darstellung und Korrelation für mehrere Merkmale

Darstellung und Korrelation für (zwei) mehrere Merkmale

In diesem Abschnitt betrachten wir stets zwei Merkmale $X:\mathrm{\Omega }\to A$ und $Y:\mathrm{\Omega }\to B$ auf derselben Grundgesamtheit $\mathrm{\Omega }$ (man spricht dann von verbundenen Merkmalen). Oft stellt sich die Frage, ob die Merkmale voneinander abhängig sind, das heißt, ob gewisse Werte für $X(\omega )$ mit gewissen anderen Werte für $Y(\omega )$ mehr bzw. weniger gehäuft auftreten. Wir wollen nun einige (gemeinsame) Darstellungsformen für zwei verbundene Merkmale angeben und Methoden behandeln, mit denen man ihre Abhängigkeit untersuchen kann.

Verbundene Merkmale

Ist $\mathrm{\Omega }=\{{\omega }_1,\dots ,{\omega }_n\}$ eine Grundgesamtheit und sind $X:\mathrm{\Omega }\to A$ und $Y:\mathrm{\Omega }\to B$ verbundene Merkmale, so bezeichnet man die Abbildung $$(X,Y):\mathrm{\Omega }\to A\times B,\omega \mapsto (X(\omega ),Y(\omega ))$$
als zweidimensionales Merkmal. Ein Wertepaar $(X({\omega }_i),Y({\omega }_i))(i=1,\dots ,n)$ heißt Beobachtungswert.

Beispiel verbundene Merkmale

• Gibt $X$ die Größe und $Y$ das Gewicht einer Person an, so wird man erwarten, dass bei einem hohen Wert $X(\omega )$ auch eher ein hoher Wert für $Y(\omega )$ auftritt.
• Ist $X$ die Regenmenge (für bestimmte Tage im Sommer) und $Y$ die Durchschnittstemperatur, so lässt sich (vermutlich) ein umgekehrter Zusammenhang erwarten (eine hohe Regenmenge entspricht eher einer niedrigen Temperatur).
• Falls $X$ die Größe einer Person und $Y$ die Punktzahl in einer Mathematik-Klausur beschreibt, so erwartet man, dass die Beobachtungswerte unabhängig voneinander sind (von Zufälligigkeiten abgesehen).

Urliste

Als Urliste bezeichnet man die Tabelle

$$\begin{array}{cccc}{\omega }_i& {\omega }_1& \dots & {\omega }_n\\ \text{X(}{\omega }_i)& \text{X(}{\omega }_1)& \dots & \text{X(}{\omega }_n)\\ \text{Y(}{\omega }_i)& \text{Y(}{\omega }_1)& \dots & \text{Y(}{\omega }_n)\end{array}$$

beziehungsweise die Auflistung aller Paare von Beobachtungswerten $$(X({\omega }_1),Y({\omega }_1)),(X({\omega }_2),Y({\omega }_2)),\dots ,(X({\omega }_n),Y({\omega }_n)).$$
als Urliste.

Wir schreiben im Folgenden auch kurz $x_i=X({\omega }_i)$ und $y_i=Y({\omega }_i)$.

Beispiel Urliste bei verbundenem Merkmal

Auf einem Bauernhof werden Hühnereier in Güteklassen (A,B und C) und Gewichtsklassen (S,M,L,XL) eingeteilt. Eine Serie von $500$ Eiern wird diesbezüglich statistisch erfasst. Auf der Grundgesamtheit $\mathrm{\Omega }=\{{\omega }_1,{\omega }_2,\dots ,{\omega }_{500}\}$ haben wir also die Merkmale $$X:\mathrm{\Omega }\to \left\{\text{A,B,C}\right\}(\text{Güte})\text{und}Y:\mathrm{\Omega }\to \left\{\text{S,M,L,XL}\right\}(\text{Gewicht})$$ Die Urliste könnte nun wie folgt aussehen:

$$\begin{array}{ccccccccc}\omega & {\omega }_1& {\omega }_2& {\omega }_3& {\omega }_4& {\omega }_5& \dots & {\omega }_{499}& {\omega }_{500}\\ \text{X(}\omega )& \text{A}& \text{A}& \text{C}& \text{B}& \text{C}& \dots & \text{B}& \text{A}\\ \text{Y(}\omega )& \text{XL}& \text{L}& \text{L}& \text{S}& \text{M}& \dots & \text{M}& \text{L}\end{array}$$

Kontingenztabellen

Gemeinsame absolute und relative Häufigkeit

Sind $X,Y:\mathrm{\Omega }\to ℝ$ verbundene Merkmale auf einer Grundgesamtheit $\mathrm{\Omega }$ mit den Merkmalsräumen $A=\{a_1,\dots ,a_m\}$ (für $X$) und $B=\{b_1,\dots ,b_{\ell }\}$ (für $Y$), so kann man wie zuvor auch die absoluten und relativen Häufigkeiten der beiden einzelnen Merkmale erfassen. An ihnen kann man aber keine Abhängigkeiten der beiden Merkmale feststellen. Man betrachtet daher die gemeinsamen absoluten bzw. relativen Häufigkeiten. Für $i=1,\dots ,m$ und $j=1,\dots ,l$ bezeichnet man
$$h_{i,j}=h(a_i,b_j)=|\{\omega \in \mathrm{\Omega };(X(\omega ),Y(\omega ))=(a_i,b_j)\}|$$
als absolute Häufigkeit von $(a_i,b_j)$ und
$$r_{i,j}=r(a_i,b_j)=\frac{h_{i,j}}{|\mathrm{\Omega }|}$$
als relative Häufigkeit von $(a_i,b_j)$.

Kontingenztabelle

Die Tabellen mit diesen Werten
$$\begin{array}{cccccc}& Y& b_1& b_2& \dots & b_l\\ X& & & & & \\ \text{HLINE TBD}{a}_1& & h(a_1,b_1)& h(a_1,b_2)& \dots & h(a_1,b_{\ell })\\ a_2& & h(a_2,b_1)& h(a_2,b_2)& \dots & h(a_2,b_{\ell })\\ ⋮& & ⋮& ⋮& \ddots & ⋮\\ a_m& & h(a_m,b_1)& h(a_m,b_2)& \dots & h(a_m,b_{\ell })\end{array}\begin{array}{cccccc}& Y& b_1& b_2& \dots & b_{\ell }\\ X& & & & & \\ \text{HLINE TBD}{a}_1& & r(a_1,b_1)& r(a_1,b_2)& \dots & r(a_1,b_{\ell })\\ a_2& & r(a_2,b_1)& r(a_2,b_2)& \dots & r(a_2,b_{\ell })\\ ⋮& & ⋮& ⋮& \ddots & ⋮\\ a_m& & r(a_m,b_1)& r(a_m,b_2)& \dots & r(a_m,b_{\ell })\end{array}$$ heißen Kontingenztabellen (oder Kreuztabellen).

Beispiel Kontingenztabelle

Im Beispiel Urliste bei verbundenem Merkmal könnten diese Tabellen beispielsweise so aussehen:
$\begin{array}{ccccccc}& \text{Gewicht}& \text{S}& \text{M}& \text{L}& \text{XL}& \text{gesamt}\\ \text{Güte}& & & & & & \\ \text{HLINE TBD}\text{A}& & h(\text{A,S})=6& h(\text{A,M})=12& h(\text{A,L})=63& h(\text{A,XL})=280& h(\text{A})=361\\ \text{B}& & h(\text{B,S})=10& h(\text{B,M})=19& h(\text{B,L})=43& h(\text{B,XL})=12& h(\text{B})=84\\ \text{C}& & h(\text{C,S})=15& h(\text{C,M})=17& h(\text{C,L})=20& h(\text{C,XL})=3& h(\text{C})=55\\ \text{HLINE TBD}\text{gesamt}& & h(\text{S})=31& h(\text{M})=48& h(\text{L})=126& h(\text{XL})=295& n=500\end{array}$
$\begin{array}{ccccccc}& \text{Gewicht}& \text{S}& \text{M}& \text{L}& \text{XL}& \text{gesamt}\\ \text{Güte}& & & & & & \\ \text{HLINE TBD}\text{A}& & r(\text{A,S})=0.012& r(\text{A,M})=0.024& r(\text{A,L})=0.126& r(\text{A,XL})=0.560& r(\text{A})=0.722\\ \text{B}& & r(\text{B,S})=0.020& r(\text{B,M})=0.038& r(\text{B,L})=0.086& r(\text{B,XL})=0.024& r(\text{B})=0.168\\ \text{C}& & r(\text{C,S})=0.030& r(\text{C,M})=0.034& r(\text{C,L})=0.040& r(\text{C,XL})=0.006& r(\text{C})=0.110\\ \text{HLINE TBD}\text{gesamt}& & r(\text{S})=0.062& r(\text{M})=0.096& r(\text{L})=0.252& r(\text{XL})=0.590& 1\end{array}$

Anmerkungen Kontingenztabelle I

• Summiert man zu einem festen $j\in \{1,\dots ,l\}$ die absoluten/relativen Häufigkeiten $h_{1,j},\dots ,h_{m,j}$, so erhält man die absolute/relative Häufigkeit der Merkmalsausprägung $b_j$ für das Merkmal $Y$, es gilt also
  $$\sum _{i=1}^{m}h(a_i,b_j)=h(b_j)\text{und}\sum _{i=1}^{m}r(a_i,b_j)=r(b_j).$$
  Analog gilt
  $$\sum _{j=1}^{l}h(a_i,b_j)=h(a_i)\text{und}\sum _{j=1}^{l}r(a_i,b_j)=r(a_i).$$
  

Anmerkungen Kontingenztabelle II

• Es gilt
  $$\sum _{i=1}^m\sum _{j=1}^l{h}_{i,j}=|\mathrm{\Omega }|\text{und}\sum _{i=1}^m\sum _{j=1}^l{r}_{i,j}=1.$$
  
• Kontinenztabellen eignen sich besonders für qualitative Merkmale. Gibt es viele mögliche Merkmalsausprägungen, so kann man diese in Klassen einteilen und dann eine Kontingenztabelle mit den Klassenhäufigkeiten erstellen.

Bedingte relative Häufigkeiten und Unabhängigkeit

Bedingte relative Häufigkeiten

Sind $X,Y:\mathrm{\Omega }\to ℝ$ verbundene Merkmale auf einer Grundgesamtheit $\mathrm{\Omega }$ mit den Merkmalsräumen $A$ und $B$, so heißt
$$r(a|b)=\frac{h(a,b)}{h(b)}(a\in A,b\in B)$$
bedingte relative Häufigkeit von $a$ unter der Bedingung $b$. Analog heißt
$$r(b|a)=\frac{h(a,b)}{h(a)}(a\in A,b\in B)$$
bedingte relative Häufigkeit von $b$ unter der Bedingung $a$

Beispiel bedingte relative Häufigkeiten

Im Beispiel Urliste bei verbundenem Merkmal ist:

• $r(S|A)=0.017<0.062=r(S)$
  Der Anteil der Eier vom Gewicht S ist unter den Eiern der Güte A kleiner (als insgesamt).
• $r(C|L)=0.159>0.110=r(C)$
  Der Anteil der Eier der Güte C ist unter den Eiern vom Gewicht L größer (als insgesamt).
• $r(A|XL)=0.949>0.722=r(A)$
  Der Anteil der Eier der Güte A ist unter den Eiern vom Gewicht XL größer (als insgesamt).

Unabhängigkeit

Man nennt nun zwei Merkmale $X,Y$ unabhängig voneinander, falls für alle Merkmalsausprägungen $a\in A$ und $b\in B$ die folgenden äquivalenten Bedingungen erfüllt sind: $r(b|a)=r(b)\iff r(a,b)=r(a)\cdot r(b)\iff r(a|b)=r(a)$

Anmerkung Unabhängigkeit

• Die Bedingung $r(b|a)=r(b)$ besagt, dass die Merkmalsausprägung $b$ "unter der Bedingung $a$" (d.h. wenn man nur die Untersuchungseinheiten $\omega$ betrachtet, bei denen $X(\omega )=a$ ist) die gleiche relative Häufigkeit hat, die sie auch insgesamt hat. Man könnte sagen: Das Auftreten von $a$ hat keinen Einfluss auf das Auftreten von $b$.

• Dieses Konzept der Unabhängigkeit ist allerdings für die Praxis nicht zu gebrauchen. Die Bedingung $r(a,b)=r(a)\cdot r(b)$ wird im Allgemeinen nicht erfüllt sein, selbst wenn die beiden Merkmale offensichtlich unabhängig voneinander sind.

Beispiel Unabhängigkeit

Ein Würfel und eine Münze werden $100$-mal geworfen (jeweils gleichzeitig). Das Merkmal $X$ gibt die Zahl des Würfels an, das Merkmal $Y$ das Ergebnis des Münzwurfs. Es ergibt sich die folgende Kontingenztabelle: $$\begin{array}{ccccccccc}& X& 1& 2& 3& 4& 5& 6& \text{gesamt}\\ Y& & & & & & & & \\ \text{HLINE TBD}\text{Kopf (K)}& & h(\text{K},1)=10& h(\text{K},2)=11& h(\text{K},3)=6& h(\text{K},4)=5& h(\text{K},5)=6& h(\text{K},6)=7& h(\text{K})=45\\ \text{Zahl (Z)}& & h(\text{Z},1)=5& h(\text{Z},2)=9& h(\text{Z},3)=15& h(\text{Z},4)=7& h(\text{Z},5)=12& h(\text{Z},6)=7& h(\text{Z})=55\\ \text{HLINE TBD}\text{gesamt}& & h(1)=15& h(2)=20& h(3)=21& h(4)=12& h(5)=18& h(6)=14& n=100\end{array}$$

Beispiel Unabhängigkeit II

Daraus erhält man beispielsweise:

• $r(\text{K})=0.45$ sowie $r(\text{K}|3)=\frac{6}{21}=0.286$ und $r(\text{K}|6)=\frac{7}{14}=0.5$

• $r(1)=0.15$ sowie $r(1|\text{K})=\frac{10}{45}=0.222$ und $r(1|\text{Z})=\frac{5}{55}=0.091$

Die Merkmale $X$ und $Y$ sind also nicht unabhängig.

Beispiel Unabhängigkeit III

Aber:

Man kann hier sicher davon ausgehen, dass sich der Würfel- und der Münzwurf gegenseitig nicht beeinflussen und daher als unabhängig anzusehen sind. Die beobachteten Unterschiede zwischen den relativen Häufigkeiten und den bedingten relativen Häufigkeiten, können hier nur als zufällige Abweichungen erklärt werden.

Frage:
Wie kann man man in einem realen Fall (zum Beispiel in 1.2) entscheiden, ob die berechnete Abhängigkeit zwischen zwei Merkmalen auf Zufall oder auf einen tatsächlich vorhandenen Zusammenhang zurückzuführen ist?

Beispiel Unabhängigkeit III

Innerhalb der schließenden Statistik gibt es Methoden, mit denen man die Unabhängigkeit zweier Größen untersuchen kann. Dabei betrachtet man die Unterschiede zwischen den relativen Häufigkeiten und den bedingten relativen Häufigkeiten auch quantitativ. Außerdem spielt die Zahl $n$ der vorhandenen Daten eine wichtige Rolle — bei großem $n$ werden die Abweichungen mit höherer Wahrscheinlichkeit klein ausfallen, daher müssen sie dann stärker gewichtet werden. Diese Fragen werden in der Vorlesung ’Statistik für Anwender II’ behandelt.

Punktwolke

Für verbundene quantitative Merkmale $X,Y:\mathrm{\Omega }\to ℝ$ nennt man ein Koordinatensystem mit den Punkten $(X(\omega ),Y(\omega ))$ für $\omega \in \mathrm{\Omega }$ Punktewolke zu $𝐗$ und $𝐘$.

Beispiel Punktwolke

Urliste

Wir betrachten die Merkmale Größe (cm) $X:\mathrm{\Omega }\to ℝ$ und Gewicht (kg) $Y:\mathrm{\Omega }\to ℝ$ auf einer Menge von Personen $\mathrm{\Omega }=\{{\omega }_1,\dots ,{\omega }_{20}\}$ mit der folgenden Urliste: $$\begin{array}{ccccccccccccccccccccc}{\omega }_i& {\omega }_1& {\omega }_2& {\omega }_3& {\omega }_4& {\omega }_5& {\omega }_6& {\omega }_7& {\omega }_8& {\omega }_9& {\omega }_{10}& {\omega }_{11}& {\omega }_{12}& {\omega }_{13}& {\omega }_{14}& {\omega }_{15}& {\omega }_{16}& {\omega }_{17}& {\omega }_{18}& {\omega }_{19}& {\omega }_{20}\\ \text{X(}{\omega }_i)& 176& 181& 183& 194& 165& 168& 177& 171& 182& 185& 174& 181& 180& 166& 174& 177& 195& 174& 176& 159\\ \text{Y(}{\omega }_i)& 80& 85& 89& 98& 58& 66& 86& 73& 75& 89& 80& 82& 85& 72& 73& 81& 101& 88& 73& 52\end{array}$$

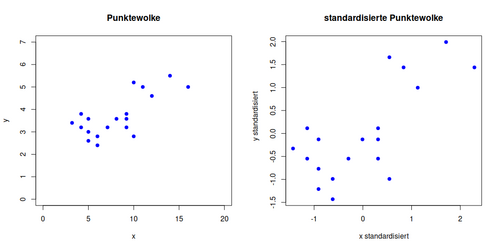
Punktwolke

Dabei ergibt sich die folgende Punktewolke (mit verschiedenen Skalierungen der Achsen):

Um eine von der Skalierung der Achsen unabhängige Darstellung zu erhalten, kann man die Merkmale standardisieren (vergleiche [Merkmale]). Die Punktewolke zu $\hat{X}$ und $\hat{Y}$ nennt man dann die standardisierte Punktewolke zu $𝐗$ und $𝐘$.

Urliste für standardisiertes Merkmal

In obigem Beispiel ergibt sich für die standardisierten Merkmale $\hat{X}$ und $\hat{Y}$:

$$\begin{array}{ccccccccccc}{\omega }_i& {\omega }_1& {\omega }_2& {\omega }_3& {\omega }_4& {\omega }_5& {\omega }_6& {\omega }_7& {\omega }_8& {\omega }_9& {\omega }_{10}\\ \hat{X}({\omega }_i)& -0.10& 0.47& 0.70& 1.97& -1.37& -1.02& 0.01& -0.68& 0.59& 0.93\\ \hat{Y}({\omega }_i)& 0.06& 0.48& 0.82& 1.59& -1.81& -1.13& 0.57& -0.54& -0.37& 0.82\end{array}$$

$$\begin{array}{ccccccccccc}{\omega }_i& {\omega }_{11}& {\omega }_{12}& {\omega }_{13}& {\omega }_{14}& {\omega }_{15}& {\omega }_{16}& {\omega }_{17}& {\omega }_{18}& {\omega }_{19}& {\omega }_{20}\\ \hat{X}({\omega }_i)& -0.33& 0.47& 0.36& -1.25& -0.33& 0.01& 2.08& -0.33& -0.10& -2.06\\ \hat{Y}({\omega }_i)& 0.06& 0.23& 0.48& -0.62& -0.54& 0.14& 1.84& 0.74& -0.54& -2.32\end{array}$$

Standardisierte Punktewolke

Damit erhält man die standardisierte Punktewolke:

Punktwolke: Anforderung an Skala

Punktewolken sind nur für quantitative Merkmale sinnvoll, da die Skalierungen der Achsen bestimmte Abstände zwischen den verschiedenen Merkmalsausprägungen suggerieren.

Punktwolke: Erstellung in R

In R: Man erstellt Vektoren x und y mit den Daten von $X$ und $Y$ und kann dann mit plot(x,y) eine Punktewolke zu $(X,Y)$ erzeugen.

Pearsonscher Korrelationskoeffizient

Linearer Zusammenhang zwischen zwei Merkmalen

Gesucht ist eine Methode zur Feststellung, ob zwei verbundene quantitative Merkmale $X,Y:\mathrm{\Omega }\to ℝ$ auf eine der beiden folgenden Arten zusammenhängen:

• $Y(\omega )\approx a\cdot X(\omega )+b$ mit $a>0$ ($X,Y$ sind positiv korreliert)
  Dabei gilt: Je größer $X(\omega )$ ist, desto größer ist $Y(\omega )$.
• $Y(\omega )\approx a\cdot X(\omega )+b$ mit $a<0$ ($X,Y$ sind negativ korreliert)
  Dabei gilt: Je größer $X(\omega )$ ist, desto kleiner ist $Y(\omega )$.

Linearer Zusammenhang und Punktwolke

Betrachten wir die standardisierte Punktewolke zu $X$ und $Y$.

• Liegen entsprechende Werte für $X$ und $Y$ gleichviele Standardabweichungen über bzw. unter dem Mittelwert, so erhält man einen Punkt auf der ersten Winkelhalbierenden.
• Liegt ein Wert für $X$ gleichviele Standardabweichungen über bzw. unter dem Mittelwert wie der entsprechenden Wert von $Y$ darunter (und umgekehrt), so erhält man einen Punkt auf der zweiten Winkelhalbierenden.

Produkt der standardisierten Beobachtungswerte

Im Allgemeinen liegen die Punkte natürlich nicht genau auf einer der Winkelhalbierenden. Man betrachtet das Produkt der standardisierten Beobachtungswerte $\hat{X}(\omega )\cdot \hat{Y}(\omega )$ zum selben Merkmalsträger $\omega$. Dieses ist

• positiv, wenn überdurchschnittliche Werte von $X$ und $Y$ zusammenfallen und wenn unterdurchschnittliche Werte von $X$ und $Y$ zusammenfallen.
• negativ, wenn überdurchschnittliche Werte von $X$ mit unterdurchschnittlichen Werten von $Y$ zusammenfallen oder umgekehrt.

Bestimmung des Pearsonschen Korrelationskoeffizient

Man summiert für alle vorhandenen Merkmalsträger $\omega \in \mathrm{\Omega }$ und teilt das Ergebnis durch die Anzahl $n$ der Punkte (man bildet also das arithmetische Mittel der Produkte der standardisierten Beobachtungswerte). Man definiert:

Für zwei verbundene quantitative Merkmale $X,Y:\mathrm{\Omega }=\{{\omega }_1,\dots ,{\omega }_n\}\to ℝ$ heißt $$r_{X,Y}=\frac{1}{n}\cdot \sum _{i=1}^n(\hat{X}({\omega }_i)\cdot \hat{Y}({\omega }_i))$$
Pearsonscher Korrelationskoeffizienten von $𝐗$ und $𝐘$.

Zusammenhnag Korrelationskoeffizient und Kovarianz

Es gilt: $r_{X,Y}=\overline{(\hat{X}\cdot \hat{Y})}=\overline{(\frac{X-\stackrel{‾}{X}}{s_X}\cdot \frac{Y-\stackrel{‾}{Y}}{s_Y})}=\frac{\overline{X\cdot Y}-\bar{X}\cdot \bar{Y}}{s_X\cdot s_Y}$
Man nennt den Zähler auf der rechten Seite auch Kovarianz von $𝐗$ und $𝐘$: $$s_{X,Y}=\overline{X\cdot Y}-\bar{X}\cdot \bar{Y}=\overline{(X-\stackrel{‾}{X})\cdot (Y-\stackrel{‾}{Y})}=\frac{1}{n}\cdot \sum _{i=1}^n(X({\omega }_i)-\bar{X})\cdot (Y({\omega }_i)-\bar{Y})$$ Offenbar gilt $s_{X,X}={s_X}^2$.

Beispiel Pearsonscher Korrelationskoeffizient

Für die beiden Merkmale $X\widehat{=}$ ’Größe’ und $Y\widehat{=}$ ’Gewicht’ aus [wolke] gilt:
$$r_{X,Y}=0.905$$

Pearsonscher Korrelationskoeffizient und Art des linearen Zusammenhangs

Es gilt stets $-1\le r_{X,Y}\le 1$, wobei: $$\begin{array}{ccc}{r}_{X,Y}=1& \iff & \text{es existieren}a,b\in ℝ\text{mit}a>0,\text{so dass}Y=aX+b\\ r_{X,Y}=-1& \iff & \text{es existieren}a,b\in ℝ\text{mit}a<0,\text{so dass}Y=aX+b\end{array}$$

Ein Korrelationskoeffizient nahe bei

$1$

deutet also an, dass ein positiver linearer Zusammenhang zwischen den beiden Merkmalen besteht.

(In obigem Beispiel zeigt der Korrelationskoeffizienten $r_{X,Y}=0.905$ also einen positiven linearen Zusammenhang zwischen $X$ und $Y$.)

Umgekehrt deutet ein Korrelationskoeffizient nahe bei

$-1$

an, dass ein negativer linearer Zusammenhang zwischen den beiden Merkmalen besteht.

Beispiel 1

Korrelationskoeffizient: $r_{X,Y}=0.724$

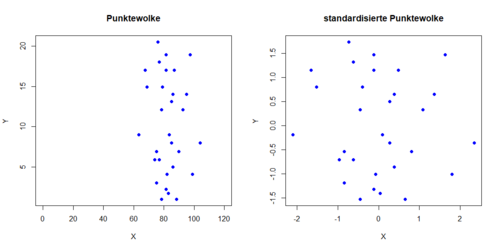
Beispiel 2

Korrelationskoeffizient: $r_{X,Y}=-0.07$

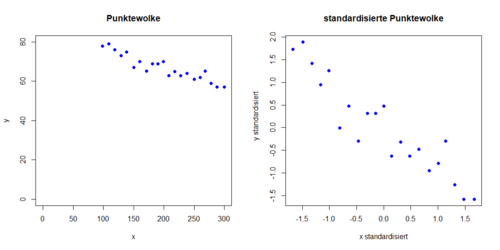
Beispiel 3

Korrelationskoeffizient: $r_{X,Y}=-0.932$

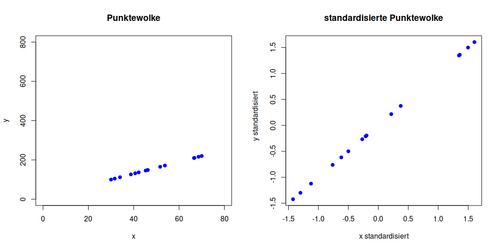
Beispiel 4

Korrelationskoeffizient: $r_{X,Y}=-0.604$

Beispiel 5

Korrelationskoeffizient: $r_{X,Y}=0.590$

Beispiel 6

Korrelationskoeffizient: $r_{X,Y}=1$

Korrelation und Ursache-Wirkungs-Prinzip

Auch wenn

$r_{X,Y}\approx 1$

oder

$r_{X,Y}\approx -1$

ist, lässt sich keine Aussage über ein "Ursache-Wirkungs-Prinzip" zwischen den beiden Größen machen. Es ist denkbar, dass eine direkt auf die Andere einwirkt. Beide Größen könnten aber auch von weiteren Umständen in gleicher (oder entgegengesetzter) Weise beeinflusst werden, oder es könnte sogar ein kompliziertes Netz von Ursachen und Wirkungen zwischen vielen verschiedenen Faktoren bestehen. Zusätzlich ist es möglich, dass der aufgrund des Korrelationskoeffizienten vermutete Zusammenhang lediglich auf Zufall zurückzuführen ist. Der Korrelationskoeffizient beschreibt (wie alles in der beschreibenden Statistik) nur die vorhandenen Daten. Diese hängen von der zufällig ausgewählten Grundgesamtheit

$\mathrm{\Omega }$

ab.

Korrelationskoeffizient nahe 0

Ein Korrelationskoeffizient nahe $0$ kann bedeuten, dass die Merkmale unabhängig voneinander sind. Genauer bedeutet es aber, dass kein linearer Zusammenhang zwischen beiden Merkmalen festgestellt wurde:

Nimmt ein Merkmal $X$ die Werte $-k,-k+1\dots ,k-1,k$ an und ist $Y=X^2$, so ergibt sich $r_{X,Y}=0$, obwohl $X$ und $Y$ ganz und gar nicht unabhängig sind ($Y$ lässt sich ja aus $X$ berechnen).

Berechnung des Korrelationskoeffizienten in R

In R: Man erstellt Vektoren x und y mit den Daten von $X$ und $Y$ und kann dann mit cor(x,y) den Korrelationskoeffizienten $r_{X,Y}$ berechnen.

Rangkorrelationskoeffizient von Spearman

Um einen monotonen Zusammenhang zwischen zwei Merkmalen $X,Y:\mathrm{\Omega }\to ℝ$ nachzuweisen, kann der Rangkorreltaionskoeffizient von Spearman verwendet werden. Hierfür muss zunächst der Rang $r_i$, also die Stelle festgestellt werden, an welcher die Beobachtung $x_i$ in der geordneten Urliste steht. Wenn die Beobachtung $x_i$ mehrfach auftritt, wird der Durchschittsrang verwendet.

Beispiel Bestimmung des Ranges

Gegeben seien die Merkmale $$x_1=40,x_2=40,x_3=31,x_4=23,x_5=31,x_6=40$$ Daraus ergeben sich die Rangsummen $$r_1=5,r_2=5,r_3=2.5,r_4=1,r_5=2.5,r_6=5$$

Definition Rangkorreltaionskoeffizient

Der Rangkorreltaionskoeffizient $r_s$ ergibt sich aus den den Rängen $r_i$ des Merkmals $X$ und den Rängen $s_i$ des Merkmals $Y$ mit einer Stichprobengröße $n$: $$r_s=\frac{\sum _{i=1}^n(r_i-\overline{r})\cdot (s_i-\overline{s})}{\sqrt{\sum _{i=1}^n(r_i-\overline{r}{)}^2\cdot \sum _{i=1}^n(s_i-\overline{s}{)}^2}}$$
Wenn keine Bindungen (Mehrfachauftreten von Werten) vorliegen, kann der Rangkorrelationskoeffizient auch bestimmt werden durch:
$$r_s=1-\frac{6\cdot \sum _{i=1}^n(r_i-s_i{)}^2}{n\cdot (n^2-1)}$$

Rangkorrelationskoeffizient und Art des Zusammenhangs

Besteht ein perfekt monoton wachsender Zusammenhang zwischen den beiden Merkmalen, so ist $r_s=1$. Ist hingegen $r_s=-1$, so liegt ein perfekt fallender monotoner Zusammenhang vor.

Beispiel Bestimmung des Rangkorrelationskoeffizient

Es werden die Noten im Abitur und vom Bachelor von $n=6$ Studierenden betrachtet und es soll ermittelt werden, ob ein monotoner Zusammenhang vorliegt:

$$\begin{array}{ccccccc}\text{Studi}& x_1& x_2& x_3& x_4& x_5& x_6\\ \text{Abitur-Note}& 1.7& 2.4& 2.0& 1.1& 2.9& 3.1\\ \text{Bachelor-Note}& 2.2& 2.4& 2.1& 1.8& 2.7& 2.6\end{array}$$

Daraus ergeben sich die folgenden Ränge:

$$\begin{array}{ccccccc}\text{Studi}& x_1& x_2& x_3& x_4& x_5& x_6\\ \text{Abitur-Note}& 2& 4& 3& 1& 5& 6\\ \text{Bachelor-Note}& 3& 4& 2& 1& 6& 5\end{array}$$

und daraus resultierend ein Rangkorrelationskoeffizient $r_s=0.89$

Rangkorrelationskoeffizient und Ursache-Wirkungs-Prinzip

Ebenso wie beim Pearsonschen Korrelationskoeffizient bedeutet eine perfekt monoton fallender oder wachsender Zusammenhang nicht direkt ein Ursache-Wirkungs-Prinzip.

Berechnung Rangkorrelationskoeffizient in R

In R: Um den Rangkorrelationskoeffizient nach Spearman zu bestimmen, geht man vor wie beim Pearsonschen Korrelationskoeffizient und nutzt das zusätzlichen Argument method = spearman : Man erstellt also Vektoren x und x mit den Daten von $X$ und $Y$ und erhält mit cor(x,y,method="spearman") den Rangkorrelationskoeffizienten $r_s$ nach Spearman.

Lineare Regression

Seien $X,Y:\mathrm{\Omega }\to ℝ$ quantitative Merkmale mit einem Korrelationskoeffizienten $r_{X,Y}\approx \pm 1$. Dann kann man von einem ungefähren linearen Zusammenhang zwischen $X$ und $Y$ ausgehen. Es existieren also $a,b\in ℝ$ (mit $a=0$) mit $Y\approx aX+b$.

Bestimmung der Regressionsgeraden

Wir wollen nun $a,b$ so bestimmen, dass diese Approximation möglichst gut ist. Eine Möglichkeit besteht darin, die Summe der Quadrate der Abweichungen
$$\text{SQA}=\sum _{i=1}^n{(aX({\omega }_i)+b-Y({\omega }_i))}^2$$
durch geeignete Wahl von $a$ und $b$ zu minimieren. Dies gelingt mit
$$a=a_0=\frac{s_{X,Y}}{{s_X}^2}\text{und}b=b_0=\bar{Y}-a_0\bar{X}$$
Die Gerade mit der Gleichung
$$y=a_{0}x+b_0$$
heißt Gerade der linearen Regression von $Y$ auf $X$ (Regressionsgerade), ihre Steigung $a_0$ Regressionskoeffizient.

Beispiel Bestimmung der Regressionsgeraden

Für die beiden Merkmale $X\widehat{=}$ ’Größe’ und $Y\widehat{=}$ ’Gewicht’ aus [wolke] gilt:
$$a_0=1.225\text{und}{b}_0=-137.40$$
Die Gerade mit der Gleichung $y=1.225x-137.40$ in der Punktewolke von $X$ und $Y$:

Regressionsgerade und Ursache-Wirkungs-Prinzip

Die Berechnung der Regressionsgeraden von

$Y$

auf

$X$

ist nur dann sinnvoll, wenn man begründet davon ausgehen kann, dass

$Y$

(in linearer Weise) von

$X$

abhängt (

$X$

ist also Ursache und

$Y$

Wirkung).

Trendgröße und Realgröße

Aus dem Prädiktor $X$ lässt sich die Trendgröße $\tilde{Y}=a_{0}X+b_0$ berechnen. Sie gibt an, welchen Wert man für $Y$ erwarten kann, wenn man den entsprechenden Wert von $X$ zugrundelegt. Da aber neben $X$ noch weitere Umstände auf $Y$ einwirken, gibt es einen Unterschied zwischen Trendgröße $\tilde{Y}$ und der Realgröße $Y$. Die Trendgröße kann aber eine sinnvolle Annäherung an die Realgröße sein, insbesondere bei einem Korrelationskoeffizienten nahe $\pm 1$ (bzw. wenn eine lineare Abhängigkeit plausibel ist). Man sollte auch überlegen, für welche Werte von $X$ eine Berechnung von $\tilde{Y}$ Sinn überhaupt macht.

Beispiel Trendgröße und Realgröße

In obigem Beispiel ist $\tilde{Y}=1.225\cdot X-137.40$.
Damit berechnet man:

$$\begin{array}{cccccccc}\text{Größe }X& 80& 150& 160& 170& 180& 190& 300\\ \text{erwartetes Gewicht }\tilde{Y}& -39.40& 46.35& 58.60& 70.85& 83.10& 95.35& 230.10\\ & \text{nicht sinnvoll}& & & & & & \text{nicht sinnvoll}\end{array}$$

Vergleich Regression X auf Y und Y auf X

Es ist natürlich auch möglich $Y$ als Prädiktor (Ursache) anzusehen und die Regressionsgerade von $X$ auf $Y$ zu bestimmen. Ein Vergleich der beiden Regressionsgeraden ergibt:

X ist Prädiktor

Gerade der linearen Regression von $Y$ auf $X$:
$y=\frac{s_{X,Y}}{{s_X}^2}\cdot x+(\bar{Y}-\frac{s_{X,Y}}{{s_X}^2}\cdot \bar{X})$ $\iff x=\frac{{s_X}^2}{s_{X,Y}}\cdot y+(\bar{X}-\frac{{s_X}^2}{s_{X,Y}}\cdot \bar{Y})$

Y ist Prädiktor

Gerade der linearen Regression von $X$ auf $Y$:

$x=\frac{s_{X,Y}}{{s_Y}^2}\cdot y+(\bar{X}-\frac{s_{X,Y}}{{s_Y}^2}\cdot \bar{Y})$ $\iff y=\frac{{s_Y}^2}{s_{X,Y}}\cdot x+(\bar{Y}-\frac{{s_Y}^2}{s_{X,Y}}\cdot \bar{X})$

Auswahl des Prädiktor

Beide Geraden stimmen nur dann überein, wenn

$r_{X,Y}=\pm 1$

ist.

Es macht also einen Unterschied, welche der beiden Größen man als Ursache und welche als Wirkung ansieht. Vor der Berechnung einer Regressionsgeraden sollte man dazu Überlegungen anstellen.

Beispiel Vergleich Regression X auf Y und Y auf X

In obigem Beispiel ist $a=0.669\text{ und }b=123.85$.
Also ergibt die Regression von $X$ auf $Y$: $x=0.669y+123.85$ bzw. äquivalent $y=1.495x-185.13$. Das folgende Diagramm zeigt die Punktewolke mit beiden Regressionsgeraden:

Hierbei scheint die Regression des Gewichts $Y$ auf die Größe $X$ mehr Sinn zu machen, da die Größe Auswirkungen auf das Gewicht hat, aber nicht umgekehrt.

Aufgabe I

In einer Studie zur Untersuchung von Herzkreislauferkrankungen wurde bei 6 Männern der Body-Maß-Index (BMI $=$ Gewicht in kg/(Körpergröße in cm)$2^{}$) ermittelt und der (systolische) Blutdruck gemessen. Es wurden folgende Daten ermittelt: $$\begin{array}{ccccccc}\text{BMI}X& 27& 23& 27& 28& 24& 25\\ \text{Blutdruck}Y& 170& 150& 160& 185& 155& 150\end{array}$$

1. Stellen Sie die Gleichung der Regressionsgerade von $Y$ auf $X$ auf und zeichnen Sie die Gerade in die Punktewolke ein.

Aufgabe I Fortsetzung

2. Stellen Sie auch die Gleichung der Regressionsgerade von $X$ auf $Y$ auf und zeichnen Sie die Gerade in die Punktwolke ein.
3. Vergleichen sie die beiden Regressionsgeraden.
4. Welchen Blutdruck erwartet man (gemäß dieser Geraden), bei einem BMI von $26$ bzw. von $19$. Begründen Sie, welchen dieser beiden Werte Sie eher als zuverlässige Schätzung ansehen würden?
5. Beurteilen Sie die Anwendbarkeit der Modelle.
6. Bestimmen Sie beide Korrelationskoeffizienten (Pearson und Spearman) von $X$ und $Y$.
7. Welche Gemeinsamkeiten/Unterschiede gibt es zwischen Spearman’s Rho und dem Korrelationskoeffizient nach Pearson?

Aufgabe II

Bearbeiten Sie zur Wiederholung von Kapitel 1 die Aufgabe im R-Skript im Materialordner. Rechnen Sie die Aufgaben sowohl mit R als auch "zu Fuß".

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Darstellung%20und%20Korrelation%20f%C3%BCr%20mehrere%20Merkmale
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.