Kurs:Statistik für Anwender/Binomialverteilte Zufallsvariable

Binomialverteilte ZV

Wahrscheinlichkeitsrechnung

Zufallsexperiment

Wir betrachten ein (wiederholbares) ZE, das $n$-mal durchgeführt wird. Bei jeder Durchführung wird beobachtet, ob ein bestimmtes (vorher festgelegtes) Ereignis eintritt oder nicht. Abkürzend sagt man: $$\mathbf{\text{''Treffer''}}\text{Das Ereignis tritt ein.}$$
$$\mathbf{\text{''KeinTreffer''}}\text{Das Ereignis tritt nicht ein.}$$
Wichtig ist dabei, dass die einzelnen Durchführungen

• unabhängig voneinander sind
• unter gleichen Bedingungen stattfinden

Zufallsvariable T

Man fasst den gesamten Vorgang nun als ein ZE auf. Die ZV $T$, die die Anzahl der Treffer beschreibt, nennt man dann binomialverteilt mit Versuchszahl $n\in \mathbb{N}$ und Trefferwahrscheinlichkeit $p\in [0,1]$ und es gilt: $$P(T=k)=(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}\text{für }k\in \{0,\dots ,n\}$$

Begründung

Dies lässt sich wie folgt begründen:
Für eine bestimmte Abfolge von $k$ Treffern und $n-k$ Nicht-Treffern ist die Wahrscheinlichkeit (entsprechend einem Pfad in einem Baumdiagramm) das Produkt aus $n$-Faktoren, von denen $k$ Faktoren $p$ sind und $n-k$ Faktoren $1-p$. Sie hat also den Wert $p^k\cdot (1-p{)}^{n-k}$.
Es gibt jedoch mehrere Pfade, in denen genau $k$ Treffer vorkommen. Da diese Treffer an $k$ von $n$ Stellen vorkommen können, sind es insgesamt $(\genfrac{}{}{0ex}{}{n}{k})$ Möglichkeiten.

Beispiel 1

Für $n=5$ und $p=0.7$ ist
$$\begin{array}{ccccccc}k& 0& 1& 2& 3& 4& 5\\ P(T=k)& 0.002& 0.028& 0.132& 0.309& 0.360& 0.168\end{array}$$

Beispiel 2.1

Für $n=50$ und $p=0.3$ ist beispielsweise:
$$\begin{array}{ccc}P(T=5)& =& 0.0005509\\ P(T=15)& =& 0.1223469\\ P(T=40)& <& 10^{-12}\end{array}$$

Wahrscheinlichkeiten

• $P(T\le k)=\sum _{j=0}^k(\genfrac{}{}{0ex}{}{n}{j})p^j(1-p{)}^{n-j}$
• $P(T\ge k)=\sum _{j=k}^n(\genfrac{}{}{0ex}{}{n}{j})p^j(1-p{)}^{n-j}$
• $P(k\le T\le \ell )=\sum _{j=k}^{\ell }(\genfrac{}{}{0ex}{}{n}{j})p^j(1-p{)}^{n-j}$

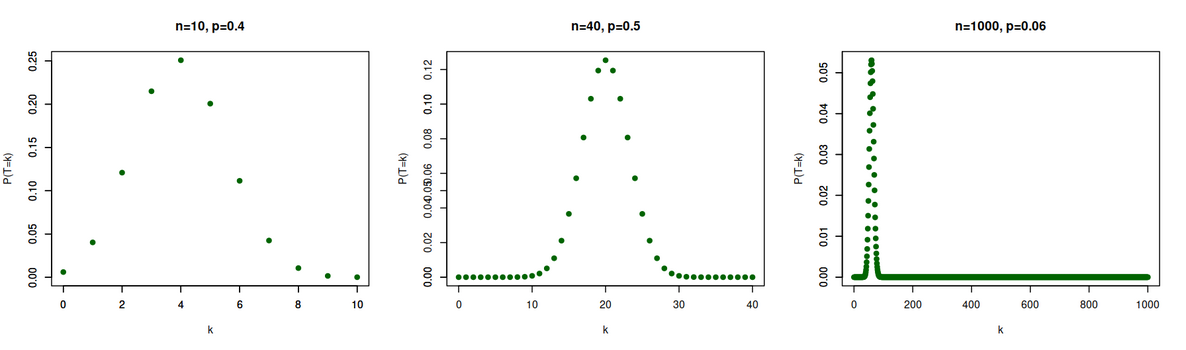
Beispiel 3

Für $n=5$ und $p=0.7$ ist beispielsweise:
$$\begin{array}{ccc}P(T\le 3)& =& 0.47148\\ P(T\ge 4)& =& 0.52852\\ P(1\le T\le 4)& =& 0.8295\end{array}$$

Beispiel 4

Für $n=50$ und $p=0.3$ ist beispielsweise: $$\begin{array}{ccc}P(6\le T\le 9)& =& 0.039509\\ P(T\le 16)& =& 0.683879\\ P(T\ge 25)& =& 0.002370\end{array}$$

Beispiel 5

Hier einige weitere Beispiele:

Beispiel 6

Interaktive App zur Binomialverteilung:

Link und Download

In R

$$\begin{array}{ccccc}\text{dbinom(}k,n,p)& \text{ergibt:}& P(T=k)& =& (\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}\\ \\ \text{pbinom(}k,n,p)& \text{ergibt:}& P(T\le k)& =& \sum _{j=0}^k(\genfrac{}{}{0ex}{}{n}{j})p^j(1-p{)}^{n-j}\\ \\ 1-\text{pbinom(}k-1,n,p)& \text{ergibt:}& P(T\ge k)& =& \sum _{j=k}^n(\genfrac{}{}{0ex}{}{n}{j})p^j(1-p{)}^{n-j}\\ \\ \text{pbinom(}\ell ,n,p)-\text{pbinom(}k-1,n,p)& \text{ergibt:}& P(k\le T\le \ell )& =& \sum _{j=k}^{\ell }(\genfrac{}{}{0ex}{}{n}{j})p^j(1-p{)}^{n-j}\end{array}$$

Aufgabe 1

Berechnen Sie für eine binomialverteilte ZV $T$ mit den jeweils angegebenen Werten für $n$ und $p$ die angegebenen Wahrscheinlichkeiten:

• Für $n=8$ und $p=0.46$: $P(T=k)$ für alle $k=0,\dots ,8$
• Für $n=24$ und $p=0.12$: $P(T\le 4),P(T\ge 6),P(2\le T\le 5)$
• Für $n=360$ und $p=0.77$: $P(T\le 275),P(T\ge 280),P(276\le T\le 280)$

Beispiele für Binomialverteilung 1

• (Ziehen mit Zurücklegen) Aus einer Lostrommel, die $N$ Kugeln enthält, von denen $K$ rot sind, werden nacheinander mit Zurücklegen $n$ Kugeln gezogen. Die ZV für die Anzahl roten Kugeln unter den Gezogenen ist binomialverteilt mit Versuchszahl $n$ und Trefferwahrscheinlichkeit $p=\frac{K}{N}$.
• Wenn man $1000$-mal würfelt, ist die ZV für die Zahl der gewürfelten $6$-en binomialverteilt mit Versuchszahl $n=1000$ und Trefferwahrscheinlichkeit $p=\frac{1}{6}$.

Beispiele für Binomialverteilung 2

• Wenn ein Medikament, das mit einer Wahrscheinlichkeit von $0.2\mathrm{\%}$ eine bestimmte Nebenwirkung verursacht, von $300$ Patienten eingenommen wird, ist die ZV für die Zahl der Patienten, bei denen die Nebenwirkung auftritt, binomialverteilt mit Versuchszahl $n=300$ und Trefferwahrscheinlichkeit $p=0.002$.

Beispiele für Binomialverteilung 3

• Wenn ein Basketballspieler $n$ Freiwürfe macht, ist die ZV für die Zahl seiner Treffer nur unter folgenden Annahmen binomialverteilt:
  • Es gibt eine Trefferwahrscheinlichkeit $p\in [0,1]$, die immer gleich groß ist.
  • Treffer bzw. Nicht-Treffer bei bestimmten Würfen beeinflussen nicht die Trefferwahrscheinlichkeit für die anderen Würfe.

Beispiele für Binomialverteilung 4

• Die Wahrscheinlichkeit für eine Mädchengeburt betrage $0.487$. Unter $200$ Neugeborenen ist dann die ZV für die Zahl der Mädchen binomialverteilt mit Versuchszahl $n=200$ und Trefferwahrscheinlichkeit $p=0.486$.

Beispiel Aufgaben 1

• Bei einem Multiple-Choice Test gibt es bei jeder der 20 Fragen 4 Antwortmöglichkeiten, von denen genau eine Antwort richtig ist. Ein unvorbereiteter Teilnehmer kreuzt willkürlich jeweils eine Antwort an. Wie groß ist die Wahrscheinlichkeit, dass er $$\text{(i) mindestens 10 Fragen}\text{(ii) weniger als 8 Fragen}$$
  $$\text{(iii) zwischen 2 und 5 Fragen}$$
  richtig beantwortet?
• Wie groß ist die Wahrscheinlichkeit beim 10-maligen Werfen von 2 Würfeln $$\text{(i) genau 2-mal}\text{(ii) mindestens 4-mal}\text{(iii) weniger als 7-mal}$$ die Augensumme $5$ zu erzielen?

Beispiel Aufgaben 2

• Auf dem Weg zur Arbeit ist eine Ampel jeden Tag mit der Wahrscheinlichkeit $p=0.4$ rot. Berechnen Sie die Wahrscheinlichkeit, dass die Ampel an genau $k$ von 7 Tagen Rot ist $(k=0,\dots ,7)$.
• Ein Bäcker knetet in einen Teig für 100 Rosinenbrötchen 200 Rosinen gut unter. Dann wird der Teig in 100 gleiche Teile geschnitten. Mit welcher Wahrscheinlichkeit enthält ein rein zufällig ausgewähltes Brötchen dieser Charge $$\text{(i)}\text{genau 2}\text{(ii)}\text{mehr als 3}\text{(iii)}\text{keine}$$
  Rosinen?
  Zusatzfrage: Wie viele Rosinen muss der Bäcker in den Teig für 100 Rosinenbrötchen kneten, damit ein auf gut Glück ausgewähltes Brötchen mit einer Mindestwahrscheinlichkeit von $0.95$ mindestens eine Rosine enthält?

Erwartungswert und Varianz einer binomialverteilten ZV

Für eine binomialverteilte ZV $T$ mit Versuchszahl $n$ und Trefferwahrsch. $p$ gilt: $$E(T)=n\cdot p\text{und}V(T)=n\cdot p\cdot (1-p)$$

EW und Varianz der relativen Häufigkeit

Ist $T$ eine binomialverteilte ZV mit Versuchszahl $n\in \mathbb{N}$ und Trefferwahrscheinlichkeit $p\in [0,1]$, so beschreibt die ZV $R=\frac{T}{n}$ die relative Häufigkeit des Ereignisses "Treffer" in der Versuchsserie.

Es gilt: $E(R)=p\text{und}V(R)=\frac{p\cdot (1-p)}{n}$

Beispiel 1

Für $n=5$ und $p=0.7$ haben wir oben bereits die Wahrscheinlichkeitsverteilung bestimmt. Daraus ergibt sich:
$$\begin{array}{ccc}E(T)& =& 0.002\cdot 0+0.028\cdot 1+0.132\cdot 2+0.309\cdot 3+0.360\cdot 4+0.168\cdot 5\\ & =& 3.5\\ V(T)& =& \left\{\begin{array}{c}0.002\cdot (0-3.5{)}^2+0.028\cdot (1-3.5{)}^2\\ +0.132\cdot (2-3.5{)}^2+0.309\cdot (3-3.5{)}^2+0.360\cdot (4-3.5{)}^2+0.168\cdot (5-3.5{)}^2\end{array}\right\}\\ & =& 1.05\end{array}$$
Tatsächlich ist $E(T)=5\cdot 0.7$ und $V(T)=5\cdot 0.7\cdot (1-0.7)$.

Beispiel 2.1

Für $n=20$ und $p=0.61$ berechnen wir zunächst $P(T=k)=(\genfrac{}{}{0ex}{}{20}{k})(0.61{)}^k(0.39{)}^{20-k}$ für alle möglichen Werte $k=0,\dots ,20$:
$$\begin{array}{cccccccc}k& 0& 1& 2& 3& 4& 5& 6\\ P(T=k)& <0.0001& <0.0001& <0.0001& <0.0001& 0.0002& 0.0010& 0.0038\\ \text{HLINE TBD}k& 7& 8& 9& 10& 11& 12& 13\\ P(T=k)& 0.0118& 0.0299& 0.0624& 0.1073& 0.1526& 0.1790& 0.1722\\ k& 14& 15& 16& 17& 18& 19& 20\\ P(T=k)& 0.1347& 0.0843& 0.0412& 0.0152& 0.0040& 0.0007& 0.0001\\ \text{HLINE TBD}\end{array}$$

Beispiel 2.2

Daraus ergibt sich:
$$\begin{array}{ccc}E(T)& =& 12.2\\ V(T)& =& 4.758\end{array}$$
Tatsächlich ist $E(T)=20\cdot 0.61$ und $V(T)=20\cdot 0.61\cdot (1-0.61)$.

Aufgabe 1

Sie werfen eine Münze 20 mal. Bestimmen Sie die folgenden Wahrscheinlichkeiten (Kopf ist "Treffer"):

• $P(T=7)$
• $P(T\le 8)$
• $P(T\ge 9)$
• $P(T<10)$
• $P(5\le T\le 15)$

Aufgabe 2

Bei dem Spiel Kniffel würfeln Sie mit fünf Würfeln (normalerweise bis zu dreimal, dies soll der Einfachheit wegen vernachlässigt werden). Wie hoch ist die Wahrscheinlichkeit,

1. ein Kniffel (fünf Gleiche) zu würfeln.
2. einen Vierer-Pasch (mindestens zwei Vierer) zu werfen.

Bestimmen Sie auch Erwartungswert und Varianz für das Werfen einer bestimmten Zahl.

Schätzungen für p

Problemstellung

Bisher können wir die Wahrscheinlichkeit dafür berechnen, dass die Trefferzahl in einem bestimmten Bereich liegt, wenn wir die Trefferwahrscheinlichkeit $p$ kennen. In der Praxis ist man häufig aber mit folgender Situation konfrontiert: $$\text{Es sind }n\text{ und }k\text{ bekannt, aber nicht }p\text{.}$$

$\text{Wie kann man }p\text{ sinnvoll schätzen?}$

Unterscheidung

Genauer kann man unterscheiden:

• Die Versuchszahl $n\in \mathbb{N}$ steht fest und ist bekannt. (In vielen Fällen kann man $n$ sogar selbst festlegen.)
• Die Trefferwahrscheinlichkeit $p\in [0,1]$ liegt fest, ist aber nicht bekannt.
• Die Trefferzahl ist zufällig.

Situation vor und nach der Datenerhebung

Sie wird vor Erhebung der Daten durch die ZV $T$ beschrieben. Nach der Datenerhebung liegt dann eine Realisierung $T^{\ast }=k\in \{0,\dots ,n\}$ der ZV $T$ vor.

Schätzungen für $p$ können nur auf der konkreten Realisierung (Trefferzahl) $T^{\ast }=k$ basieren. Da der Schätzung also die zufällige Trefferzahl $T$ zugrunde liegt, ist folglich auch die Schätzung vom Zufall abhängig.
$$\text{ZV mit Parameter p}\stackrel{\text{zufällig}}{⟶}\text{Daten k }\stackrel{\text{methodisch}}{⟶}\text{Schätzung für p}$$

Punktschätzung für p

Sei $T$ eine binomialverteilte ZV mit (bekannter) Versuchszahl $n\in \mathbb{N}$ und (unbekannter) Trefferwahrscheinlichkeit $p\in [0,1]$.

Eine Punktschätzfunktion für $p$ ist eine Abbildung:

$$\begin{array}{cccc}S:& \underset{\text{Menge der möglichen Werte für die ZV T}}{\underbrace{\{0,\dots ,n\}}}& \to & \underset{\text{(Ober-)Menge der in Frage kommenden Werte von p}}{\underbrace{ℝ}}\\ & \underset{\text{konkrete Trefferzahl}}{\underbrace{k}}& \mapsto & \underset{\text{konkrete Schätzung für p}}{\underbrace{S(k)}}\end{array}$$

Punktschätzfunktion vor und nach Datenerhebung

Eine solche Punktschätzfunktion kann aus verschiedenen Blickwinkeln betrachtet werden:

• Vor der Durchführung des ZE ist die Trefferzahl $T$ eine ZV. Da die Trefferzahl in die Schätzfunktion eingesetzt werden soll, kann man so auch die Schätzung selbst als ZV $S\widehat{=}S(T)$ interpretieren.
• Nach dem Feststellen einer konkreten Trefferzahl $T^{\ast }=k$ kann man diese einfach in die Schätzfunktion einsetzen und erhält so in der Praxis eine konkrete Schätzung $S(k)$ für $p$.

Beispiel 1.1

(Relative Häufigkeit ist Punktschätzfunktion für $p$) Die Abbildung:
$$R:\{0,\dots ,n\}\to ℝ,R(k)=\frac{k}{n}$$
ist eine Punktschätzfunktion für $p$.
Es stellt sich nun die Frage nach einer sinnvollen Punktschätzfunktion für $p$ (es liegt nahe, die relative Häufigkeit $R$ aus Beispiel Beispiel 1.1 zu betrachten) bzw. allgemeiner was überhaupt sinnvolle$$ Eigenschaften für eine solche Schätzfunktion sind. Um dies zu beurteilen, sollte man den Standpunkt vor der Datenerhebung einnehmen.

Relative Häufigkeit als Zufallsvariable

Die relative Häufigkeit ist erwartungstreu, effizient und konsistent:
Fasst man die relative Häufigkeit als Zufallsvariable auf, so gilt:

1. $R$ ist erwartungstreu für $p$, das heißt es gilt: $E_p(R)=p$ für alle $p\in [0,1]$
   Dabei ist $E_p(R)$ der (von $p$ abhängige) EW von $R$.
2. Es gilt: $V_p(R)\stackrel{n\to \mathrm{\infty }}{⟶}0$ für alle $p\in [0,1]$
   Dabei ist $V_p(R)$ die (von $p$ abhängige) Varianz von $R$.
3. $R$ ist konsistent, das heißt für alle $p\in [0,1]$ und alle $c>0$ gilt: $Pp(|R-p|<c)\stackrel{n\to \mathrm{\infty }}{⟶}1$
   

Dabei bedeutet $P_p(\dots )$ das die Wahrscheinlichkeit in Abhängigkeit von $p$ berechnet wurde.

Das Maximum-Likelihood-Prinzip

Neben den schon genannten Qualitätskriterien für Punktschätzfunktionen (Erwartungstreue, Effizienz und Konsistenz) gibt es noch einen anderen Zugang, die sogenannte Maximum-Likelihood-Methode. Dabei wird für den unbekannten Parameter (hier die Trefferwahrscheinlichkeit $p$) der Wert geschätzt, für den die beobachteten Daten (hier die Trefferzahl $T^{\ast }=k$) möglichst wahrscheinlich waren.

Maximum-Likelihood-Schätzung 1

Die Maximum-Likelihood-Schätzung $S_{ML}:\{0,\dots ,n\}\to [0,1]$ ist also wie folgt definiert:

Für $k\in \{0,\dots ,n\}$ ist $S_{ML}(k)\in [0,1]$ die (globale) Maximumstelle der Funktion $$L:[0,1]\to [0,1],L(p)=\underset{=P(T=k)\text{(abhängig von p)}}{\underbrace{(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}}}$$
($L$ steht für Likelihood-Funktion)

Maximum-Likelihood-Schätzung 2

Die Wahrscheinlichkeit $p$ wird bei $k$ Treffern in $n$ Versuchen also als der Wert geschätzt, für den die Wahrscheinlichkeit $P(T=k)$ für genau $k$ Treffer maximal ist.

Man kann zeigen, (vergleiche die folgenden Beispiele) dass stets $S_{ML}(k)=\frac{k}{n}=R(k)$ gilt. Auch mit dieser Methode erhält man also die relative Häufigkeit als sinnvolle Schätzung für $p$.

Beispiel 2

n = 50, k =10 bzw. n=400, k = 250

Intervallschätzungen für p

Ein (für die Praxis relevantes) Problem bei den bisher behandelten Punktschätzungen für $p$ ist, dass es sich bei den Gütekriterien (Erwartungstreue, Effizienz und Konsistenz) für die Schätzfunktionen lediglich um qualitative Aussagen handelt.

Ziel ist es nun, Schätzungen für $p$ zu formulieren, die man auch quantitativ beurteilen kann. Eine solche hat die Form: $$\text{Der unbekannte Wert}p\text{liegt in einem Intervall der Form}[p_U,p_O].$$

Situation

Wir betrachten die folgende Situation:
Zu einer binomialverteilten ZV $T$ ist die Versuchszahl $n\in \mathbb{N}$ fest und bekannt und die Trefferwahrscheinlichkeit $p\in [0,1]$ fest, aber unbekannt. Basierend auf der vom Zufall abhängigen Trefferzahl $T^{\ast }=k\in \{0,\dots ,n\}$ soll nun eine Intervallschätzung
$$p\in [p_U,p_O]=[p_U(k),p_O(k)]$$
für $p$ vorgenommen werden.

Betrachtung vor der Datenerhebung

Erneut nehmen wir die folgenden beiden Standpunkte ein:

Vor der Durchführung des ZE ist die Trefferzahl $T$ eine ZV. Da die Trefferzahl in die Intervallschätzfunktion eingesetzt werden soll, hängt somit auch das berechnete Intervall
$B(T)=[p_U(T),p_O(T)]$
vom Zufall ab. Damit ist es auch vom Zufall abhängig, ob die resultierende Aussage
$p\in [p_U(T),p_O(T)]$
wahr oder falsch sein wird.

Betrachtung nach der Datenerhebung

Nach dem Feststellen einer konkreten Trefferzahl $T^{\ast }=k$ kann man diese einfach in die Schätzfunktion einsetzen und erhält so in der Praxis eine konkrete Intervallschätzung
$B(k)=[p_U(k),p_O(k)]$
für $p$. Die Aussage
$p\in [p_U(k),p_O(k)]$
ist dann nicht mehr vom Zufall abhängig, sondern entweder wahr oder falsch. (Leider weiß man nicht, welcher der beiden Fälle eingetreten ist, da man $p$ nicht kennt.)

Intervallschätzung als Abbildung

Sei ${ℐ}_{[0,1]}=\{[a,b];0\le a\le b\le 1\}$ die Menge der abgeschlossenen Teilintervalle von $[0,1]$.

Eine Intervallschätzung (bzw. Bereichsschätzung) für $p$ ist eine Abbildung: $$\begin{array}{cccc}B:& \underset{\text{Menge der möglichen Werte für die ZV T}}{\underbrace{\{0,\dots ,n\}}}& \to & \underset{\begin{array}{c}\text{Menge von Teilmengen der Menge}\\ \text{aller in Frage kommenden Werte von p}\end{array}}{\underbrace{{ℐ}_{[0,1]}}}\\ & \underset{\text{konkrete Trefferzahl}}{\underbrace{k}}& \mapsto & \underset{\text{konkrete Intervallschätzung für }p}{\underbrace{B(k)=[p_U(k),p_O(k)]}}\end{array}$$

Beurteilung einer Intervallschätzung

Um Intervallschätzungen sinnvoll beurteilen zu können, untersuchen wir die (vom unbekannten Parameter $p$ abhängige) Wahrscheinlichkeit dafür, dass man ein "korrektes Intervall" (also eines, dass $p$ tatsächlich enthält) berechnet, wenn man die (vom Zufall abhängige) Trefferzahl einsetzt.

Überdeckungswahrscheinlichkeit und Konfidenzniveau

Gegeben sei eine Intervallschätzfunktion: $$B:\{0,\dots ,n\}\to {ℐ}_{[0,1]},B(k)=[p_U(k),p_O(k)]$$

Überdeckungswahrscheinlichkeit

Für einen denkbaren Parameterwert $p\in [0,1]$ definiert man die Überdeckungswahr-scheinlichkeit von $B$ an der Stelle $p$ durch:
$$P_B(p)=P(B(T)\ni p)=P([p_U(T),p_O(T)]\ni p)=\sum _{k\in \{0,\dots ,n\},B(k)\ni p}(\genfrac{}{}{0ex}{}{n}{k})\cdot p^k\cdot (1-p{)}^{n-k}$$

Anmerkung

Die Schreibweise $B(T)\ni p$ ist mathematisch gleichbedeutend zu $p\in B(T)$, hat aber den Vorteil, dass dabei deutlich wird, dass $B(T)$ (und nicht $p$) vom Zufall abhängt. Anstatt zu sagen: $p$ ist in $B(T)$ enthalten." formuliert man daher auch $B(T)$ fängt $p$ ein."

Konfidenzniveau

Gilt $P_B(p)\ge \delta$ für eine feste Zahl $\delta \in [0,1]$, so sagt man auch:
"Die Intervallschätzung $B$ hält das Konfidenzniveau $\delta$ ein."

Bedeutung 1

Die Überdeckungswahrscheinlichkeit entspricht der Wahrscheinlichkeit dafür, dass man ein korrektes Intervall erhalten wird, wenn man die zufällige Trefferzahl $T$ in die Intervallschätzung $B$ einsetzt. Da die Überdeckungswahrscheinlichkeit vom unbekannten Parameter $p$ abhängt, kann man sie in der Praxis nicht berechnen.

Bedeutung 2

Weiß man aber (aufgrund theoretischer Überlegungen), dass eine Intervallschätzung ein bestimmtes Konfidenzniveau $\delta$ einhält, so ist (unabhängig vom wahren Wert von $p$) garantiert, dass man MINDESTENS mit der Wahrscheinlichkeit $\delta$ ein korrektes Intervall erhalten wird, wenn man die zufällige Trefferzahl $T$ in die Intervallschätzung $B$ einsetzt.

In der Praxis sollte man nur Intervallschätzungen verwenden, von denen man weiß, dass sie ein hohes Konfidenzniveau (üblich sind $\delta =0.9$ oder $\delta =0.95$ oder $\delta =0.99$) einhalten.

Ziel

Wie findet man zu einem vorgegebenen Konfidenzniveau $\delta \stackrel{\text{z.B.}}{=}0.95$ eine Intervallschätzung, die dieses Konfidenzniveau garantiert einhält.

Intervallschätzung nach Clopper-Pearson

Vorgegeben sei $\delta \in ]0,1[$.

Für $k\in \{0,\dots ,n\}$ bestimmt man $p_U=p_U(k)$und $p_O=p_O(k)$aus den Gleichungen:
$$\sum _{j=k}^n(\genfrac{}{}{0ex}{}{n}{j}){p_U}^j(1-p_U{)}^{n-j}=\frac{1-\delta }{2}$$
$$\sum _{j=0}^k(\genfrac{}{}{0ex}{}{n}{j}){p_O}^j(1-p_O{)}^{n-j}=\frac{1-\delta }{2}$$
Dann hält die Intervallschätzung $B:\{0,\dots ,n\}\to {ℐ}_{[0,1]},B(k)=[p_U(k),p_O(k)]$ garantiert das Konfidenzniveau $\delta$ ein.

Ausnahmen

Ausnahme sind folgende Sonderfälle:
Für $k=0$ setze $p_U=p_U(0)=0$, für $k=n$ setze $p_O=p_O(n)=1$.

Anmerkung

Obige Bestimmungsgleichungen für $p_U$ und $p_O$ sind ohne Computereinsatz kaum zu lösen. Konfidenzintervalle nach Clopper-Pearson können aber in R direkt berechnet werden. Der Befehl
$$\text{binom.test(}k,n,\text{conf.level}=\delta )\mathrm{\$}\text{conf.int}[1:2]$$
ergibt das Konfidenzintervall zum Vertrauensniveau $\delta$ bei $k$Treffern in $n$Versuchen.

Bemerkung 1

Obergrenzen für die Wahrsch. für Über- bzw. Unterschätzung von $p$:
Die Grenzen $p_U$und $p_O$der Intervallschätzung nach Clopper-Pearson aus Satz Intervallschätzung nach Clopper-Pearson sind so gewählt, dass die Wahrscheinlichkeiten für "Unterschätzung" und "Überschätzung" von $p$ durch dieselbe Grenze beschränkt sind. Genauer: $$P\left(\underset{\text{Unterschätzung}}{\underbrace{p>p_O(T)}}\right)\le \frac{1-\delta }{2}\text{und}P\left(\underset{\text{Unterschätzung}}{\underbrace{p<p_U(T)}}\right)\le \frac{1-\delta }{2}$$

Bemerkung 2

Zusammen ergibt sich damit

$$P\left(\underset{\text{falsche Schätzung}}{\underbrace{p\notin [p_U(T),p_O(T)]}}\right)\le 1-\delta$$

und folglich

$P\left(\underset{\text{korrekte Schätzung}}{\underbrace{p\in [p_U(T),p_O(T)]}}\right)\ge \delta$

Dass man diesen Aussagen überhaupt eine Wahrscheinlichkeit zuschreiben kann, liegt daran dass die Intervallgrenzen $p_U(T)$ und $p_O(T)$ zufällig sind (und nicht etwa der unbekannte, aber feste Wert $p$).

Beispiel 1.1

Für $n=100$ und $k=71$ ergeben sich die Intervallgrenzen als Lösungen der Gleichung

$$\frac{1-\delta }{2}=\sum _{j=71}^{100}(\genfrac{}{}{0ex}{}{100}{j}){p_U}^j(1-p_U{)}^{100-j}$$

und

$\frac{1-\delta }{2}=\sum _{j=0}^{71}(\genfrac{}{}{0ex}{}{100}{j}){p_O}^j(1-p_O{)}^{100-j}$

Beispiel 1.2

Hierbei wären also Polynome vom Grad

$n=100$

aufzulösen. Mit R berechnen wir:

$$\begin{array}{c}\text{Für }\delta =0.6\text{ ist }[p_U,p_O]=[0.665,0.751].\\ \text{Für }\delta =0.8\text{ ist }[p_U,p_O]=[0.644,0.769].\\ \text{Für }\delta =0.9\text{ ist }[p_U,p_O]=[0.626,0.784].\\ \text{Für }\delta =0.99\text{ ist }[p_U,p_O]=[0.580,0.819].\end{array}$$

Beispiel 2.1

Für $n=20$ erhält man zum Konfidenzniveau $\delta =0.8$ mit der Clopper-Pearson-Methode abhängig von $k$ die folgenden (mit R berechneten) Konfidenzintervalle $B(k)=[p_U(k),p_O(k)]$:
$$\begin{array}{cccccccc}k& 0& 1& 2& 3& 4& 5& 6\\ B(k)& [0,0.109]& [0.005,0.181]& [0.027,0.245]& [0.056,0.304]& [0.090,0.361]& [0.127,0.415]& [0.166,0.467]\\ \text{HLINE TBD}k& 7& 8& 9& 10& 11& 12& 13\\ B(k)& [0.207,0.518]& [0.249,0.567]& [0.292,0.615]& [0.338,0.662]& [0.385,0.707]& [0.433,0.751]& [0.482,0.793]\\ \text{HLINE TBD}k& 14& 15& 16& 17& 18& 19& 20\\ B(k)& [0.533,0.834]& [0.585,0.873]& [0.639,0.910]& [0.696,0.944]& [0.755,0.973]& [0.819,0.995]& [0.891,1]\end{array}$$

Beispiel 2.2

Wir berechnen für verschiedene denkbare Werte von $p$, die Überdeckungswahrscheinlichkeit (also die Wahrscheinlichkeit dafür, dass die Intervallschätzung korrekt ist):

Beispiel 2.3

Angenommen, es ist $p=0.3$. Dann ist die Intervallschätzung für $T\in \{3,4,5,6,7,8,9\}$ korrekt. Die Wahrscheinlichkeit dafür ist:
$$P_B(0.3)=P(B(T)\ni 0.3)=P(3\le T\le 9)=0.917$$

Beispiel 2.4

Angenommen, es ist $p=0.52$. Dann ist die Intervallschätzung für $T\in \{8,9,10,11,12,13\}$ korrekt. Die Wahrscheinlichkeit dafür ist:
$$P_B(0.52)=P(B(T)\ni 0.52)=P(8\le T\le 13)=0.822$$

Beispiel 2.5

Angenommen, es ist $p=0.88$. Dann ist die Intervallschätzung für $T\in \{16,17,18,19\}$ korrekt. Die Wahrscheinlichkeit dafür ist: $$P_B(0.88)=P(B(T)\ni 0.88)=P(16\le T\le 19)=0.840$$

Beispiel 2.6

Angenommen, es ist $p=1$. Dann ist die Intervallschätzung für $k=20$ korrekt. Die Wahrscheinlichkeit dafür ist:
$$P_B(1)=P(B(T)\ni 1)=P(T=20)=1$$

Korrektheit der Schätzung

Es ist bewiesen, dass die Schätzung bei beliebigem $p$ immer mindestens mit der Wahrscheinlichkeit $\delta$ korrekt ist.

Größe der Konfidenzintervalle 1

Bei fester relativer Häufigkeit werden die Konfidenzintervalle mit wachsender Versuchszahl kleiner (mit mehr Versuchen erreicht man eine höhere Genauigkeit) und mit wachsendem Konfidenzniveau größer (ein höheres Konfidenzniveau "bezahlt"man mit einer ungenaueren Aussage). Man beachte die Größenordnungen dieser Veränderungen anhand der folgenden (mit R berechneten) Konfidenzintervalle:

Größe der Konfidenzintervalle 2

$$\begin{array}{ccccccc}& k/n& 3/10& 30/100& 300/1000& 3000/10000& 30000/100000\\ \delta & & & & & & \\ & & & & & & \\ 0.6& & [0.157,0.484]& [0.258,0.346]& [0.287,0.313]& [0.296,0.304]& [0.298,0.302]\\ & & & & & & \\ & & & & & & \\ 0.8& & [0.115,0.552]& [0.239,0.367]& [0.281,0.320]& [0.294,0.306]& [0.298,0.302]\\ & & & & & & \\ & & & & & & \\ 0.9& & [0.087,0.607]& [0.224,0.385]& [0.276,0.325]& [0.292,0.308]& [0.297,0.303]\\ & & & & & & \\ & & & & & & \\ 0.95& & [0.066,0.653]& [0.212,0.400]& [0.271,0.330]& [0.291,0.310]& [0.297,0.303]\\ & & & & & & \\ & & & & & & \\ 0.99& & [0.037,0.735]& [0.189,0.431]& [0.263,0.339]& [0.288,0.312]& [0.296,0.304]\\ & & & & & & \end{array}$$

Bemerkung Verwendung von Intervallschätzungen in der Praxis 1

In der Praxis ist bei der Verwendung von Intervallschätzungen wie folgt vorzugehen:

1. Zunächst macht man sich die Situation klar: Die Trefferwahrscheinlichkeit $p$ einer Binomialverteilung ist unbekannt (aber fest, d.h. nicht vom Zufall abhängig).
2. Man legt fest:

• das Verfahren, mit dem man die Intervallschätzung berechnen wird. (z.B. zweiseitiger Test nach Clopper-Pearson).

Bemerkung Verwendung von Intervallschätzungen in der Praxis 2

• eine Versuchszahl $n\in \mathbb{N}$
  zu beachten:
  Hohe Werte von $n$ führen zu einem engeren Konfidenzintervall.
• ein Konfidenzniveau $\delta \in ]0,1[$
  zu beachten:
  Hohe Werte von $\delta$ entsprechen einer höheren Untergrenze für die Wahrscheinlichkeit einer korrekten Schätzung, führen aber zu einem breiteren Konfidenzintervall. Sinnvoll ist z.B. $\delta =0.95$.

Bemerkung Verwendung von Intervallschätzungen in der Praxis 3

3. Man führt die Versuchsreihe durch und stellt die Trefferzahl $T^{\ast }=k$ fest.
Zu beachten:
Wichtig bei einer Binomialverteilung ist, dass die einzelnen Versuche unabhängig voneinander und immer unter den gleichen Bedingungen durchgeführt werden.

Bemerkung Verwendung von Intervallschätzungen in der Praxis 4

4. Man berechnet das Konfidenzintervall $[p_U(k),p_O(k)]$ mit der zuvor festgelegten Methode. (Dies kann der Computer erledigen.)

5. Man verkündet das Ergebnis:

$p\in [p_U(k),p_O(k)]\text{mit dem Zusatz: }$

" Das Konfidenzniveau

$\delta$

wurde eingehalten." Damit ist klar: Vor Erhebung der Daten war die Wahrscheinlichkeit ein korrektes Intervall zu erhalten, mindestens

$\delta$

. Nach Berechnung des Intervalls kann man damit der Aussage

$p\in [p_U(k),p_O(k)]$

ein gewisses Vertrauen entgegenbringen (aber keine Wahrscheinlichkeit zuweisen, sie ist entweder wahr oder falsch).

Bemerkung Einseitig begrenzte Konfidenzintervalle

In gewissen Situationen kann es Sinn machen, die Clopper-Pearson-Methode so zu modifizieren, dass man einseitig (statt wie bisher zweiseitig) begrenzte Konfidenzintervalle berechnet.

Beispiel 3

Ist $p$ beispielsweise die Wahrscheinlichkeit dafür, dass eine bestimmte Maßnahme einen gewünschten Erfolg erzielt, so könnte es wichtig sein, $p$ (möglichst strikt) nach unten abzuschätzen, aber eine Abschätzung von $p$ nach oben ist nicht notwendig.
Dazu kann man linkssseitig begrenzte Konfidenzintervalle verwenden.

Beispiel 4

Ist $p$ beispielsweise die Wahrscheinlichkeit dafür, dass bei der Einnahme eines Medikaments eine (unerwünschte) Nebenwirkung auftritt, so könnte es wichtig sein, $p$ (möglichst strikt) nach oben abzuschätzen, aber eine Abschätzung von $p$ nach unten ist nicht notwendig.
Dazu kann man rechtsseitig begrenzte Konfidenzintervalle verwenden.

Einseitig begrenze Konfidenzintervalle

Einseitig begrenze Konfidenzintervalle zu einem vorgegebenen Konfidenzniveau $\delta \in (0,1)$ werden wie folgt berechnet:

Linksseitig begrenzte Konfidenzintervalle

Bei $k$ Treffern aus $n$ Versuchen bestimmt man das linksseitig begrenzte Konfidenzintervall $[p_U,1]$ zum Vertrauensniveau $\delta$ durch
$$\sum _{j=k}^n(\genfrac{}{}{0ex}{}{n}{j}){p_U}^j(1-p_U{)}^{n-j}=1-\delta$$
(Sonderfall: Für $k=0$ setze $p_U=0$.)

Rechtsseitig begrenzte Konfidenzintervalle

Bei $k$ Treffern aus $n$ Versuchen bestimmt man das rechtsseitig begrenzte Konfidenzintervall $[0,p_O]$ zum Vertrauensniveau $\delta$ durch
$$\sum _{j=0}^k(\genfrac{}{}{0ex}{}{n}{j}){p_O}^j(1-p_O{)}^{n-j}=1-\delta$$
(Sonderfall: Für $k=n$ setze $p_O=1$.)

Überschätzung bei linksseitig begrenzten Konfidenzintervallen

Linksseitig begrenzte Konfidenzintervalle dürfen den Wert von $p$ mit einer Wahrscheinlichkeit von bis zu $1-\delta$ überschätzen (statt $\frac{1-\delta }{2}$ wie bei den zweiseitigen Intervallschätzungen). Um dies auszugleichen, unterschätzen sie den Wert von $p$ nie (die obere Grenze ist $1$). Die untere Grenze kann daher im Vergleich zum zweiseitigen Test etwas besser (größer) gewählt werden.

Unterschätzung bei rechtsseitig begrenzten Konfidenzintervallen

Rechtsseitig begrenzte Konfidenzintervalle dürfen den Wert von $p$ mit einer Wahrscheinlichkeit von bis zu $1-\delta$ unterschätzen (statt $\frac{1-\delta }{2}$ wie bei den zweiseitigen Intervallschätzungen). Um dies auszugleichen, überschätzen sie den Wert von $p$ nie (die untere Grenze ist $0$). Die obere Grenze kann daher im Vergleich zum zweiseitigen Test etwas besser (kleiner) gewählt werden.

Berechnung in R

In R berechnet man einseitige Konfidenzintervalle nach Clopper-Pearson mit

$\text{binom.test}$$($$\text{k,n,}\text{conf.level=delta, alternativ=}$ "$\text{greater}$ "$)\mathrm{\$}$$\text{conf.int}$$[$$1:2$$]$ $\mathrm{\#}\text{linksseitig begrenzt}$
$\text{binom.test}$$($$\text{k,n,}\text{conf.level=delta, alternativ=}$ "$\text{less}$ "$)\mathrm{\$}$$\text{conf.int}$$[$$1:2$$]$ $\mathrm{\#}\text{rechtsseitig begrenzt}$

Beispiel 5

Konfidenzintervalle im Vergleich für $k=112,n=200\Rightarrow \frac{k}{n}=0.56$:
$$\begin{array}{cccc}\delta & 0.8& 0.9& 0.95\\ \text{beidseitig begrenzt}& [0.512,0.607]& [0.499,0.620]& [0.488,0.630]\\ \text{linksseitig begrenzt}& [0.527,1]& [0.512,1]& [0.499,1]\\ \text{rechtsseitig begrenzt}& [0,0.591]& [0,0.607]& [0,0.620]\end{array}$$

Bestimmung der Intervallgrenzen

Allgemein bestimmt man aus den Gleichungen $$\sum _{j=k}^n(\genfrac{}{}{0ex}{}{n}{j}){p_U}^j(1-p_U{)}^{n-j}={\alpha }_U(\text{und}{p}_U=0,\text{falls}k=0)$$ $$\sum _{j=0}^k(\genfrac{}{}{0ex}{}{n}{j}){p_O}^j(1-p_O{)}^{n-j}={\alpha }_O(\text{und}{p}_O=1,\text{falls}k=n)$$ die Grenzen einer Intervallschätzung $[p_U,p_O]$, die den Wert von $p$ mit einer Wahrscheinlichkeit von höchstens ${\alpha }_U$ überschätzt und mit einer Wahrscheinlichkeit von höchstens ${\alpha }_O$ unterschätzt.

Konfidenzniveau der Schätzung

Das heißt, es gilt
$$P(p<p_U)\le {\alpha }_U\text{und}P(p>p_O)\le {\alpha }_O$$
und damit
$$P(p\in [p_U,p_O])\ge 1-{\alpha }_U-{\alpha }_O$$
Damit ist $\delta =1-{\alpha }_U-{\alpha }_O$ das Konfidenzniveau der Schätzung.

Beispiel 6

Für $\delta =0.95$ hat man zum Beispiel folgende Möglichkeiten:
$$\begin{array}{cccccc}& & P(p<p_U)& P(p>p_O)& P(p\notin [p_U,p_O])& P(p\in [p_U,p_O])\\ {\alpha }_U=0.025,{\alpha }_O=0.025& zweiseitig,{\alpha }_U={\alpha }_O& \le 0.025& \le 0.025& \le 0.05& \ge 0.95\\ {\alpha }_U=0.05,{\alpha }_O=0& linksseitigbegrenzt& \le 0.05& 0& \le 0.05& \ge 0.95\\ {\alpha }_U=0,{\alpha }_O=0.05& rechtsseitigbegrenzt& 0& \le 0.05& \le 0.05& \ge 0.95\\ {\alpha }_U=0.04,{\alpha }_O=0.01& zweiseitig,{\alpha }_U={\alpha }_O& \le 0.04& \le 0.01& \le 0.05& \ge 0.95\\ {\alpha }_U=0.02,{\alpha }_O=0.03& zweiseitig,{\alpha }_U={\alpha }_O& \le 0.02& \le 0.03& \le 0.05& \ge 0.95\end{array}$$

Aufgabe 3.1

Bei einer bestimmten Tierart kann bei bestimmten Nachkommen eine morphologische Veränderung beobachtet werden. Die genaue Wahrscheinlichkeit $p$ dafür, dass ein neugeborenes Tier die morphologische Veränderung aufweisst, ist aber unbekannt und soll geschätzt werden.
In einer Studie werden dazu $250$ neugeborene Tiere untersucht. Von diesen Tieren weissen $180$ die morphologische Veränderung auf.

Aufgabe 3.2

1. Geben Sie anhand der Daten eine Punktschätzung für $p$ ab.
2. Stellen Sie die Maximum-Likelihood-Funktion auf
3. Es soll eine Intervallschätzung $[p_U,p_O]$ für $p$ zum Konfidenzniveau $\delta =0.9$ abgegeben werden.

• Geben Sie die Gleichungen an, anhand derer sich $p_U$ und $p_O$ bestimmen lassen (zweiseitige Intervallschätzung nach Clopper-Pearson). Verwenden Sie dazu wieder die erhobenen Daten ($180$ Nachkommen mit morphologischer Veränderung bei $250$ untersuchten). Setzen Sie alle bekannten Zahlenwerte in die Gleichungen ein.

Aufgabe 3.3

• Berechnen Sie mit R die Grenzen $p_U$ und $p_O$.
• Erklären Sie, inwiefern die Korrektheit der Intervallschätzung $p\in [p_U,p_O]$ vom Zufall abhängt. Was weiß man über die Wahrscheinlichkeit, dass die Intervallschätzung korrekt ist? Unterscheiden Sie bei Ihren Erläuterungen die Situation vor und nach der Datenerhebung (bzw. der Berechnung der Intervallgrenzen).

Aufgabe 3.4

• Wie ändert sich die Breite des Konfidenzintervalls, wenn man das Konfidenzniveau von $0.9$ auf $0.95$ erhöht?
• Wie verändert sich die Breite des Konfidenzintervalls, wenn man statt $180$ morphologisch auffälligen von $250$ untersuchten neugeborenen Tieren eine Untersuchung mit $1800$ von $2500$ untersuchten neugeborenen Tieren zugrunde legt?

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Binomialverteilte%20Zufallsvariable
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.