Kurs:Mathematische Modellbildung/Themen/Sport - Elfmeterschießen/Modellierungszyklus 3
Zur Navigation springen
Zur Suche springen
Ziel des dritten Modellierungszyklus
- Darstellung der Formel aus dem zweiten Modellierungszyklus in einem Koordinatensystem
- Erweiterung des Modells mithilfe mehrerer Faktoren, die in der Realität eine Rolle spielen
- Darstellung der erarbeiteten Funktion in einem Koordinatensystem
- Darstellung einer sogenannten Heatmap für die zu überschreitenden Geschwindigkeiten
Darstellung der Funktion aus Zyklus 2

Darstellung der Funktion aus Zyklus 2

Erläuterung der Abbildung
- zu überschreitende Geschwindigkeit vor allem im Bereich der Handpunkte schnell gegen unendlich
- Symmetrie zu erkennen, wobei die senkrechte Gerade durch die Mitte des Tors prinzipiell die Spiegelachse bildet
- zu überschreitende Geschwindigkeiten werden geringer, je weiter sie von den Handpunkten entfernt sind
Position der Hände abhängig von den Körpermaßen
- Angabe der Handpunkte in Abhängigkeit von den Körpermaßen
- je nach Köprergröße und Körperbau sind die Positionen der beiden Hände unterschiedlich
- Annahme: Hände neben dem Torwart auf Hüfthöhe
- Nutzung von , falls
- Nutzung von , falls
Strecke des Torwarts
Reaktionszeit des Torwarts
- Annahme: Torwart muss auf Schuss reagieren, bevor er seine Bewegung einleitet
- Reaktionszeit wird zur vorherigen Zeit des Torwarts bis zum Treffpunkt addiert
- mit Einbezug der erarbeiteten Handpunkte:
Einbezug der Gleichung in die Ungleichung aus Zyklus 2
<
Ungleichung aus Zyklus 2
Verfeinerung der Torwartbewegung als Translation und Rotation
- in Zyklus 2 lediglich Translation der Handpunkte betrachtet
- genauere Analyse der Armbewegung
- Mischform einer Translation und eine Rotation um ein Schultergelenk
- Bewegungen werden nicht nacheinander, sondern gleichzeitig ausgeführt
- Zeit führt Gesamtbewegung ergibt sich aus dem zeitlichen Maximum der beiden Teilbewegungen
Translatorische Bewegung
- Schulterpunkte müssen betrachtet werden
- Ball dennoch mit den Händen halten
- Entfernung, die zurückgelegt werden muss ergibt sich aus dem Abstand der Schulterpunkte zum Treffpunkt, wobei davon die Armlänge subtrahiert wird
Darstellung Entfernung Translationsbewegung
Darstellung Entfernung Translationsbewegung
Zeit für Translationsbewegung
Rotatorische Bewegung
- Beschreibung der Rotationsbewegung des Armes um das Schultergelenk
- Berechnung des Winkels, der vom Arm überschritten wird
- , mit als Winkel, ω als Winkelgeschwindigkeit und t als Zeit
Rotation um die Schulterpunkte

- der Winkel, den der Arm überschreiten muss, wird von den Strecken und , beziehungsweise und eingeschlossen
Rotation um die Schulterpunkte
Zeit der Roatationsbewegung
Zeit, die der Torwart zum Treffpunkt benötigt
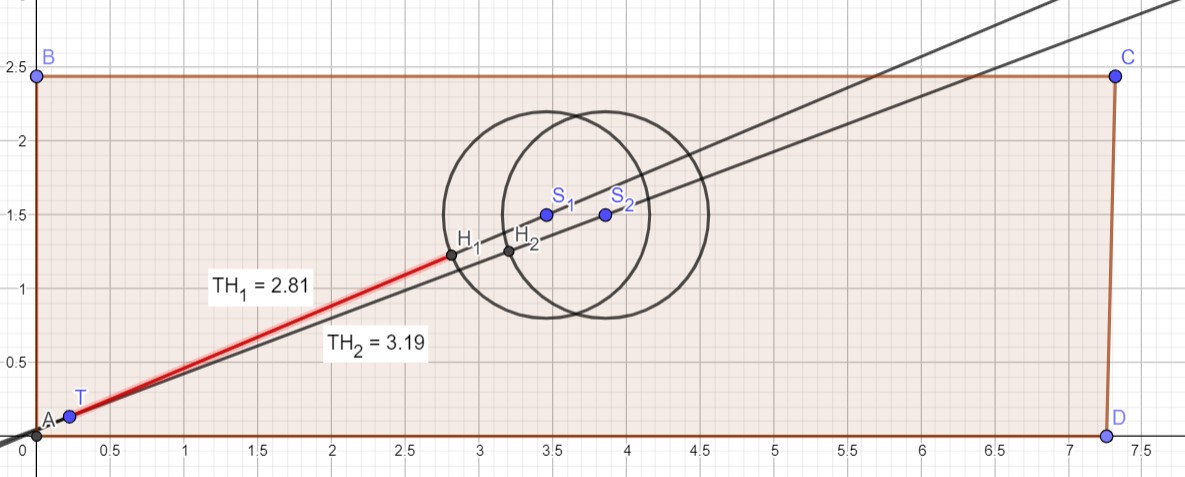
Erweiterung Trefferpunkt im Kreis der Armweite ums Schultergelenk
Befindet sich der Trefferpunkt innerhalb einer der Handkreise, so müssten wir nach unserem Modell eine Translation und eine Rotation ausführen. Da der/die Torhüter/in den Ball allerdings auch ohne eine Translation mit dem ausgestreckten Arm erreichen wird, beschränken wir die Bewegung des/der Torhüter/in in diesem Fall auf eine Rotation. Die Handkreise lassen sich wie folgt darstellen:
Veränderung von t_Torwart
Körpermaße in Abhängigkeit zur Körpergröße
- betrachtete Parameter beeinflussen die gesuchte Schussgeschwindigkeit
- zur Erleichterung: Körpermaße in Abhängigkeit zur Körpergröße k
Schussgeschwindigkeit für einen beliebigen Treffpunkt
Parameter, die die nötige Schussgeschwindigkeit beeinflussen
- Körpergröße des Torwarts
- Bewegungsgeschwindigkeit des Torwarts
- Winkelgeschwindigkeit der Arme des Torwarts
- Reaktionszeit des Torwarts
- Treffpunkt des Balles im Tor
Darstellung der Ungleichung als Funktion
- gibt gerade die Schussgeschwindigkeit an, bei der der Torwart und der Ball gleichzeitig am Treffpunkt ankommen
- es muss also gelten
Darstellung der Funktion mit festgelegten Parametern
- abgesehen vom Treffpunkt des Balles im Tor müssen zur Darstellung der Funktion im Koordinatensystem alle anderen Faktoren bekannt sein
Darstellung der Funktion mit festgelegten Parametern

Erstellung einer Heatmap für die nötige Schussgeschwindigkeit

Beispiel 1: hohe Geschwindigkeiten nötig

Beispiel 2: geringe Geschwindigkeiten nötig

Auswertung
- Ziel des dritten Zyklus: weitere Faktoren einbauen, die im realen Vorgang von Bedeutung sind und in Zyklus 2 nicht berücksichtigt wurden
- Dabei sollten die Körpergröße und die Bewegung des Torwarts weiter analysiert werden
- Die beiden Graphen in Zyklus 3 weisen eine Ähnlichkeit auf
- Im Bereich mittleren Bereich ist die zu überschreitende Schussgeschwindigkeit höher als in den Ecken
- Außerdem ist erneut eine Symmetrie bezüglich der Mitte des Tors erkennbar
Auswirkung der Parameter auf den Graphen
- Durch die Beispiele ist auch erkennbar, wie sich die Parameter des Torwarts auf den Graphen auswirken
- In Beispiel 1 wurden die Werte so gewählt, dass sehr hohe Geschwindigkeiten benötigt werden (teilweise 100m/s)
- In Beispiel 2 wurden Werte eingesetzt, die zu geringen Geschwindigkeiten führen (in den Ecken nur 6 m/s)
Aussagen über die Auswirkung der Parameter auf den Graphen
Die zu überschreitende Geschwindigkeit wächst mit:
- Größe des Torwarts
- Bewegungsgeschwindigkeit des Torwarts
- Winkelgeschwindigkeit der Arme des Torwarts
- möglichst geringer Reaktionszeit des Torwarts
Wiki2Reveal
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- [1] Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische_Modellbildung/Themen/Sport_-_Elfmeterschie%C3%9Fen/Modellierungszyklus_3
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.