Kurs:Mathematische Modellbildung/Themen/Modellierung des Infektionsgeschehens durch SARS-CoV-2/Zyklus 3

Das SI-Modell

Ein sehr einfaches Kompartiment-Modell ist die Unterteilung einer Population in lediglich zwei Kompartimente:

• Anteil der Nicht-Infizierten $S$ (Susceptible) an der Gesamtbevölkerung N: Eine Zahl zwischen 0 und 1
• Anteil der Infizierten $I$ (Infected)

In der Gruppe $I$ befinden sich Individuen, welche einmal durch den Erreger infiziert wurden (unabhängig davon, ob sie Symptome zeigen oder nicht).

Susceptibles können von dem Kompartiment $S$ durch eine Infektion in das Kompartiment $I$ wechseln.

Exponentielles Wachstum

Eine sehr einfache Annahme besteht darin, dass jeder Infizierte Susceptibles (aus einem unendlichen Vorrat) mit einer festen Rate infiziert.

$I(t)=C_e\cdot e^{\beta \cdot t}$,

also exponentielles Wachstum mit einer Infektionskontaktrate $\beta$ und $C_e$ als Anteil an Infizierten am Tag 0.

Das SIR-Modell

Beim vorigen SI-Modell infiziert ein Mitglied von $I$ mit einer konstanten Infektionskontaktrate $\beta$ "endlos" weiter.

Dies ist natürlich eine grobe Vereinfachung, der man durch die Einführung der Klasse $R$ (Removed) im Kompartiment-Modell abhelfen will.

Das SIR-Modell

Die Erhaltungsgleichung wird um den Anteil $R$ erweitert: $S+I+R=1$.

Die Infektionsfunktion übernimmt man unverändert aus dem SI-Modell.

Die Gesundungs-Funktion führt nun Anteile aus $I$ nach $R$ mit einer Genesungsrate $\gamma$ über:

$\frac{dR}{dt}=\dot{R}=f_I()=\gamma \cdot I$

Das SIR-Modell

Beim SIR-Modell kommen also zum einen neue Infizierte hinzu ($S\to I$, genauso wie beim SI-Modell), andere wechseln in die Gruppe ($I\to R$):

$\frac{dI}{dt}=\dot{I}=\dot{S}-\dot{R}=f_S()-f_I()=\beta \cdot S\cdot I-\gamma \cdot I$

Das SIR-Modell

amit haben wir ein kleines System von Differentialgleichungen mit

$\dot{S}=-\beta \cdot S\cdot I$

$\dot{I}=\beta \cdot S\cdot I-\gamma \cdot I$

$\dot{R}=\gamma \cdot I$

Wegen $R+S+I=1$ ergibt sich $\dot{R}+\dot{S}+\dot{I}=0$.

Damit ergibt sich die dritte Differentialgleichung auch aus $\dot{R}=-\dot{S}-\dot{I}$. Sie braucht daher nicht integriert zu werden.

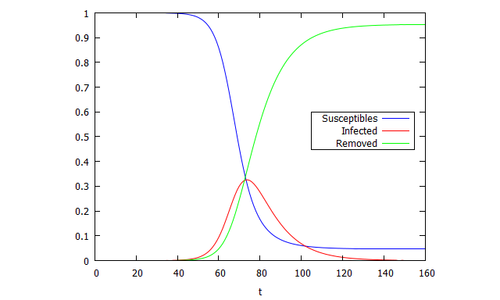
Lösung des Gleichungssystems mit Maxima

Auch Differentialgleichungssysteme lassen sich mit der rk()-Funktion leicht lösen. In den Klammern werden lediglich mehrere Gleichungen hintereinander eingefügt und durch Kommata getrennt:

/*SIR-Modell*/
beta: 0.3219;
gamma: 0.1;
I0: 1.93E-07;
sol: rk([ -beta*S*I ,
           beta*S*I-gamma*I],
           [S,I],
           [(1-I0),I0],
           [t,0,160,1])$
plot2d ([[discrete,makelist([p[1],p[2]],p,sol)],
         [discrete,makelist([p[1],p[3]],p,sol)],
         [discrete,makelist([p[1],1-p[3]-p[2]],p,sol)]] ,
         [xlabel,"t"],
         [legend,"Susceptibles","Infected","Removed"],
         [color, blue, red,green],
         [gnuplot_preamble, "set key box at 155.,.6" ])$

Die Basisreproduktionszahl

Eine oft genannte Kenngröße bei Epidemien ist die Basisreproduktionszahl $R_0$. Sie gibt an, wie viele Andere eine Infizierte Person während der Phase der Infektiosität durchschnittlich ansteckt.

Für das SIR-Modell gilt :

$R_0=\frac{\beta }{\gamma }$.

Mit den Werten für $\beta =0,3219$ und $\gamma =0,1$ würden wir als $R_0=3,219$ erhalten. Dies liegt innerhalb der Schätzwerte $2,4<R_0<3,3$.