Kurs:Statistik für Anwender/Gleichverteilte Zufallsvariablen

Gleichverteilte ZV

Seien $a,b\in ℝ$ mit $a<b$ gegeben.

Definition gleichverteilte Zufallsvariable

Eine ZV $X$ mit der W-Dichte $f:ℝ\to [0,\mathrm{\infty }),f(t)=\{\begin{array}{ccc}\frac{1}{b-a}& ,& \text{falls}t\in [a,b]\\ 0& ,& \text{sonst}\end{array}$
heißt gleichverteilt auf dem Intervall $[a,b]$.

Verteilungsfunktion gleichverteilte Zufallsvariable

Für die Verteilungsfunktion

$F$

von

$X$

gilt dann:

$$F(x)=\underset{-\mathrm{\infty }}{\overset{x}{\int }}f(t)dt=\{\begin{array}{ccc}0& ,& \text{falls}x\in ]-\mathrm{\infty },a[\\ \frac{x-a}{b-a}& ,& \text{falls}x\in [a,b]\\ 1& ,& \text{falls}x\in ]b,\mathrm{\infty }[\end{array}$$

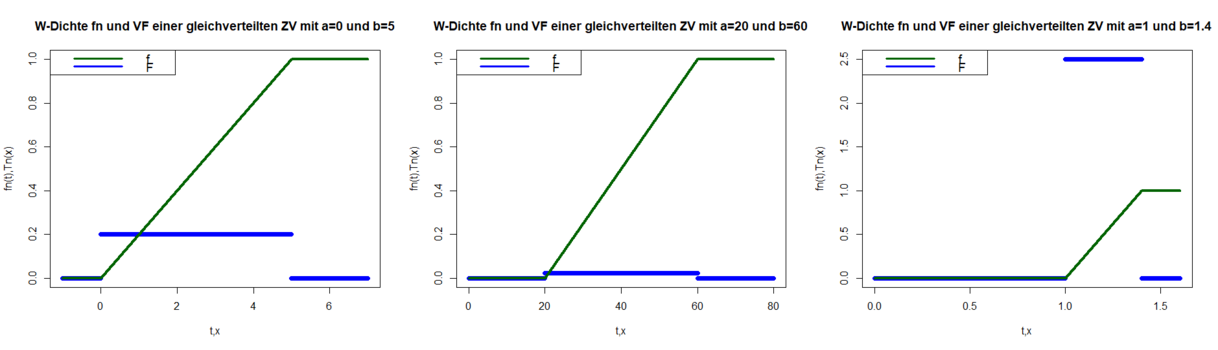
Beispiel gleichverteilte Zufallsvariable

Beispiel gleichverteilte Zufallsvariable interaktiv

Interaktive Shiny-App zur Gleichverteilung:
Download und Link

Wahrscheinlichkeit gleichverteilte Zufallsvariable

Für eine auf dem Intervall $[a,b]$ gleichverteilte ZV $X$ gilt: $P(a\le X\le b)=1$
Weiterhin gilt für beliebige Zahlen $u,v\in ℝ$ mit $a\le u\le v\le b$:
$$P(u\le X\le v)=\frac{v-u}{b-a}$$
Die Gleichverteilung kann also als Modell verwendet werden, wenn $Z$ nur Werte in $[a,b]$ annehmen kann und mit gleicher Wahrscheinlichkeit in alle gleich großen Teilbereiche fällt.

Erwartungswert und Varianz gleichverteilte Zufallsvariable

Für eine auf dem Intervall $[a,b]$gleichverteilte ZV $X$ gilt: $$E(X)=\frac{a+b}{2}\text{und}V(X)=\frac{(b-a{)}^2}{12}$$

Praktische Anwendung gleichverteilte Zufallsvariable

In bestimmten Situationen ist es naheliegend, gleichverteilte ZV als Modell zu verwenden:

• Eine ZV, die den Winkel (im Bogenmaß bzw. im Gradmaß) beschreibt, den der Zeiger eines Glücksrad mit einer festen Markierung einschließt, kann plausibel durch eine Gleichverteilung (auf $[0,2\pi ]$ bzw. auf $[0,360]$) beschrieben werden.

• In einer Stadt fährt eine U-Bahn alle 5 Minuten. Die Wartezeit auf die Bahn (in Minuten) bei zufälligem Eintreffen am Bahnsteig kann plausibel durch eine auf $[0,5]$ gleichverteilte ZV beschrieben werden.

Beispiel I

Für eine auf $[0,20]$ gleichverteilte ZV $Z$ gilt $$P(Z\le 8)=0.4,P(Z\ge 15)=0.25,$$ $$P(3\le Z\le 16)=0.65,$$ $$P(-4\le Z\le 22)=1$$
Außerdem ist $E(Z)=10$ und ${\sigma }_Z=5.7735$.

Beispiel II

Für eine auf $[-8,8]$ gleichverteilte ZV gilt: $$P(2\le Z\le 10)=0.375=P(2\le Z),$$ $$P(-12\le Z\le -4)=0.25=P(Z\le -4)$$

Außerdem ist $E(Z)=0$ und ${\sigma }_Z=\frac{16}{\sqrt{12}}=4.6188$.

Gleichverteilte Zufallsvariable in R

Für eine auf dem Intervall $[a,b]$-gleichverteilte ZV $X$ berechnet man in R:

• die Funktionswerte der W-Dichte von $X$ durch: $f(t)=dunif(t,a,b)$
• die Funktionswerte der VF von $X$ durch: $F(x)=punif(x,a,b)$
• die Wahrscheinlichkeit für $X\in [u,v]$ durch: $P(u\le X\le v)=punif(v,a,b)-punif(u,a,b)$

Aufgabe I

Seien

$a$

,

$b\in ℝ$

mit

$a<b$

. Betrachten Sie die Funktion

$$f:ℝ\to ℝ,\text{ mit }f(t)=\{\begin{array}{c}\frac{1}{b-a},\text{ falls }t\in [a,b],\\ 0,\text{ sonst}\end{array}$$

1. Skizzieren Sie den Graphen von $f$ für verschiedene Werte von $a$ und $b$ (evtl. auch mit R).
2. Zeigen Sie, dass $f$ eine W-Dichte ist.
3. Überlegen Sie Beispiele für Zufallsexperimente, die durch eine ZV mit der W-Dichte $f$ beschrieben werden können.
4. Wie sieht die Verteilungsfunktion einer solchen ZV $X$ aus? Geben Sie die Funktionsvorschrift an und skizzieren Sie die Funktion.
5. Sei $X$ eine stetige ZV mit der W-Dichte $f$ für $a=0$ und $b=10$. Berechnen Sie die Wahrscheinlichkeiten $P(1\le X\le 4)$, $P(4<X\le 12)$, $P(X<2)$, $P(X\ge 0)$ und $P(X>10)$.

Aufgabe II

Gegeben sei die gleichverteilte ZV $Z$ auf dem Intervall $[-8,8]$. Bestimmen Sie

1. $P(2\le Z\le 10)$
2. $P(-12\le Z\le -4)$
3. $P(Z\ge 7)$
4. $P(Z\le 3)$
5. $P(Z=8)$
6. Erwartungswert $E(Z)$
7. Varainz $V(Z)$
8. Standardabweichung ${\sigma }_Z$

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Gleichverteilte%20Zufallsvariablen
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.