Kurs:Funktionalanalysis/Satz des Thales

Aus testwiki
Version vom 15. Juli 2024, 15:49 Uhr von imported>Fath7937 (→Beweis 1 - Orthogonalität der Katheten)
(Unterschied) ← Nächstältere Version | Aktuelle Version (Unterschied) | Nächstjüngere Version → (Unterschied)
Zur Navigation springen Zur Suche springen

Einleitung

Satz des Thales
Geometrische Darstellung des Satzes des Thales im (Prä-)Hilbertraum.

Diese Seite kann als Wiki2Reveal Folien angezeigt werden. Einzelne Abschnitte werden als Folien betrachtet und Änderungen an den Folien wirken sich sofort auf den Inhalt der Folien aus. Den Satz des Thales auf Prähilberträume zu übertragen ist dabei nur eine Option der Verallgemeinerung[1].

Zielsetzung

Diese Lernressource hat das Ziel, den Satz des Thales in (Prä-)Hilbert-Räumen zu beweisen. Dabei gibt es eine zusätzlich Einschränkung in (Prä-)Hilbert-Räumen über den komplexen Zahlen, die so aus der euklidschen Geometrie der Eben nicht bekannt sind.

Zielgruppe

Die Zielgruppe der Lernressource sind Lehramtstudierende, die die Verallgemeinerung von Sätzen aus der Sekundarstufe I auf Hilbert-Räumen kennen lernen möchten.


Satz des Thales

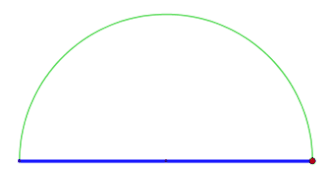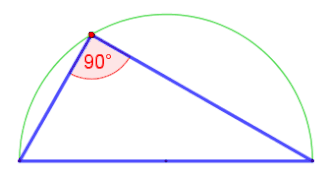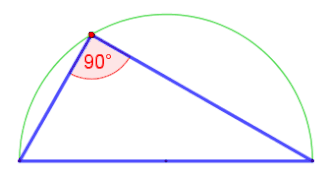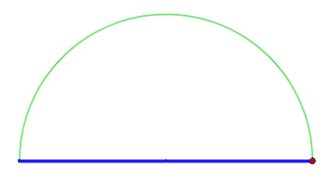
Sei (V,⟨⋅,⋅⟩) ein Prä-Hilbert-Raum über 𝕂=ℝ,ℂ. Das Dreieck wird durch folgende Vektoren dargestellt.

  • AB→=2⋅w ("Durchmesser Kreis") und AM→=w
  • AC→=v1, BC→=v2, MC→=r mit ‖w‖=‖r‖.
  • für Prä-Hilberträume über ℂ verlangt man ferner ⟨w,r⟩∈ℝ.

Dann gilt ⟨v1,v2⟩=0 (d.h. das Dreieck rechtwinklig).

Beweis

In dem Beweis zeigen wir über die Eigenschaften des Skalarproduktes, dass die Katheten in dem Dreieck senkrecht aufeinander stehen. Sei (V,⟨⋅,⋅⟩) ein Prä-Hilbert-Raum über 𝕂=ℝ,ℂ. Dabei liefert die Eigenschaft ‖w‖=‖r‖, das die Ecken des Dreieck auf einem Kreis liegen.

Bemerkung zur Übertragung in (Prä-)Hilbert-Räume

Die bekannten geometrischen Eigenschaften aus der Ebene wurden dabei wie folgt auf (Prä-)Hilbert-Räume übertragen:

  • AB→=2⋅w und AM→=w, bedeutet, dass M der Mittelpunkt der Strecke AB‾ ist.
  • AC→=v1, BC→=v2 sind die Katheten des Dreiecks,
  • Durch MC→=r und ‖w‖=‖r‖ liegt der Punkt C auf einem Halbkreis mit dem Radius ‖r‖.

Beweis 1 - Orthogonalität der Katheten

Man berechnet nun ⟨v1,v2⟩ durch Einsetzung und Anwendung der Eigenschaften des Skalarproduktes:

⟨v1,v2⟩=⟨w+r,−w+r⟩=⟨w+r,−w⟩+⟨w+r,r⟩=(−⟨w,w⟩⏟=‖w‖2−⟨r,w⟩)+(⟨w,r⟩+⟨r,r⟩⏟=‖r‖2)=−‖w‖⏟=‖r‖2+⟨r,w⟩−⟨r,w⟩‾⏟=⟨r,w⟩∈ℝ+‖r‖2=0

Beweis 2 - Orthogonalität der Katheten

Damit gilt ⟨v1,v2⟩=0 und das Dreieck mit den obigen Katheten v1,v2 und der Hypotenuse 2⋅w ist rechtwinklig. ◻

Aufgaben für Studierende

  • Formulieren und beweisen Sie die Umkehrung auf (Prä-)Hilbert-Räumen, bei der nach Vorausetzung in einem rechtwinkligen Dreieck der Punkt C in dem Dreieck ⟨A,B,C⟩, an dem ein rechter Winkel vorliegt, auf einem Halbkreis über der Hypotenuse AB‾ liegt.

Literatur/Quellennachweise

  1. ↑ G. Weiß, F.Gruber (2008), Den Satz von THALES verallgemeinern - aber wie?, Scientific and Professional Journal of the Croatian Society for Geometry and Graphics, KoG•12–2008, S. 8-18


Siehe auch

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionalanalysis' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Abgerufen von „https://de.wikiversity.beta.math.wmflabs.org/w/index.php?title=Kurs:Funktionalanalysis/Satz_des_Thales&oldid=1369“