Kurs:Funktionalanalysis/Skalarproduktnorm

Einführung

Eine Skalarproduktnorm, Innenproduktnorm oder Hilbertnorm ist in der Mathematik eine von einem Skalarprodukt induzierte (abgeleitete) Norm. In einem endlichdimensionalen reellen oder komplexen Vektorraum mit dem Standardskalarprodukt entspricht die Skalarproduktnorm gerade der euklidischen Norm.

Prähilbertraum und Norm

Allgemein besitzt jeder Prähilbertraum eine zugeordnete Skalarproduktnorm und ist mit dieser Norm ein normierter Raum. Eine Norm ist dabei genau dann von einem Skalarprodukt induziert, wenn sie die Parallelogrammgleichung erfüllt.

Cauchy-Schwarzsche Ungleichung

Jede Skalarproduktnorm erfüllt weiterhin die Cauchy-Schwarz-Ungleichung und ist invariant unter unitären Transformationen.

Klassifikation topologischer Räume

Definition: Prähilbertraum

Ist $V$ ein Vektorraum über den Körper $𝕂$ der reellen oder komplexen Zahlen und $⟨\cdot ,\cdot ⟩$ ein Skalarprodukt auf $V\times V$, dann ist $(V,⟨\cdot ,\cdot ⟩)$ ein Skalarproduktraum oder Prähilbertraum. Die von diesem Skalarprodukt induzierte Norm ist für einen Vektor $v\in V$ dann definiert als

$\Vert v\Vert :=\sqrt{⟨v,v⟩}$,

also die Wurzel aus dem Skalarprodukt des Vektors mit sich selbst.

Bemerkung: Wohldefiniertheit

Diese Definition ist wohldefiniert, da das Skalarprodukt eines Vektors mit sich selbst reell und nichtnegativ ist.

Zusammenhang - Topologische Räume

Diese Norm heißt auch Skalarproduktnorm, Innenproduktnorm oder Hilbertnorm und wird in reellen Skalarprodukträumen gelegentlich als (allgemeine) euklidische Norm bezeichnet. Mit der Skalarproduktnorm ist der Vektorraum $V$ ein normierter Raum $(V,\Vert \cdot \Vert )$. Weiterhin ist $V$ mit der von der Norm induzierten Metrik $d$ ein metrischer Raum $(V,d)$ und mit der Normtopologie $𝒯$ ein topologischer Raum $(V,𝒯)$.

Beispiele

Skalarprodukte können nicht nur auf den grundlegenden endlichdimensionalen Vektorräumen, wie dem ${ℝ}^n$ oder ${ℂ}^n$ definiert werden. Wichtige Beispiele für Skalarproduktnormen werden nun genannt.

Euklidische Norm

Die euklidische Norm auf dem euklidischen Raum der endlichdimensionalen Vektoren,

Skalarproduktnorm auf Folgenräumen

Die ℓ²-Norm auf dem Raum ℓ² der quadratisch summierbaren Folgen,

L²-Norm auf Vektorräume von Funktionen

Die L²-Norm auf dem Raum L² der quadratisch Lebesgue-integrierbaren Funktionen,

Sobolev-Norm

Die Sobolev-Norm auf dem Sobolev-Raum H^s der Funktionen, deren gemischte schwache Ableitungen bis zum Grad $s$ quadratisch Lebesgue-integrierbar sind,

Frobenius-Norm

Die Frobenius-Norm auf dem Raum der Matrizen,

Hilbert-Schmidt-Norm

Die Hilbert-Schmidt-Norm auf dem Raum der Hilbert-Schmidt-Operatoren.

Eigenschaften

• Die durch das Skalarprodukt induzierte Abbildung $\Vert v\Vert =\sqrt{⟨v,v⟩}$ ist eine Norm.
• In einem (Prä-)Hilbertraum gilt die Parallelogrammgleichung
• In einem (Prä-)Hilbertraum gilt der Satz des Pythagoras

Normeigenschaften

Vektoren in der Dreiecksungleichung

Jede Skalarproduktnorm erfüllt die drei Normaxiome

• (N1) Definitheit,
• (N2) absolute Homogenität und
• (N3) Subadditivität bzw. Dreiecksungleichung.

Beweis N1 - Definitheit

Die Definitheit folgt für $v\in V$ aus der Eindeutigkeit der Nullstelle der Wurzelfunktion über

$\Vert v\Vert =0\iff \sqrt{⟨v,v⟩}=0\Rightarrow ⟨v,v⟩=0\iff v=0$,

Beweis N2 - Absolute Homogenität

Die absolute Homogenität folgt für $v\in V$ und $\lambda \in 𝕂$ unter Ausnutzung der Bilinearität über dem Körper $ℝ$ bzw. Sesquilinearität über $ℂ$ mit

$\Vert \lambda v{\Vert }^2=⟨\lambda v,\lambda v⟩=\overline{\lambda }\lambda ⟨v,v⟩=|\lambda {|}^2\Vert v{\Vert }^2$

Beweis: N3 - Dreiecksungleichung

Die Dreiecksungleichung (oder Subadditivität) folgt für $v,w\in V$ über die Cauchy-Schwarz-Ungleichung (siehe den folgenden Abschnitt) aus

Abschätzung der Norm

$\begin{array}{cc}\Vert v+w{\Vert }^2& =⟨v+w,v+w⟩=⟨v,v⟩+⟨v,w⟩+⟨w,v⟩+⟨w,w⟩\\ & =\Vert v{\Vert }^2+⟨v,w⟩+\overline{⟨v,w⟩}+\Vert w{\Vert }^2\\ & =\Vert v{\Vert }^2+2\mathrm{Re}⟨v,w⟩+\Vert w{\Vert }^2\le \Vert v{\Vert }^2+2\Vert v\Vert \Vert w\Vert +\Vert w{\Vert }^2\\ & ={(\Vert v\Vert +\Vert w\Vert )}^2,\end{array}$

Bemerkung zur Abschätzung

Für die Abschätzung wurde ferner verwendet, dass der Realteil $Re(z)=z_1$ einer komplexen Zahl $z=z_1+i{z}_2\in ℂ$ durch den Betrag des Realteils nach oben abgeschätzt werden kann.

$\mathrm{Re}⟨v,w⟩\le |⟨v,w⟩|\le \Vert v\Vert \cdot \Vert w\Vert$

wobei der Realteil und Imaginärteil in der komplexen Zahlebene betragsmäßig den Katheden eines rechtwickligen Dreiecks entspricht und $|z|$ der Länge der Hypothenuse.

Bemerkung Dreiecksungleichung

Abschließend wird auf die Ungleichung der nicht-negativen Terme noch die Wurzel angewendet und man erhält mit Cauchy-Schwarz die Gültigkeit der Dreiecksungleichung für die vom Skalarprodukt induzierten Norm.

Aufgabe für Lernende

Satz des Thales

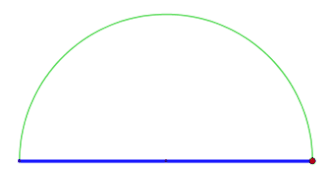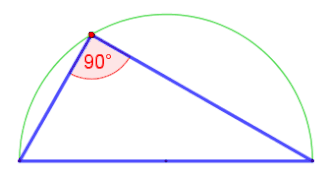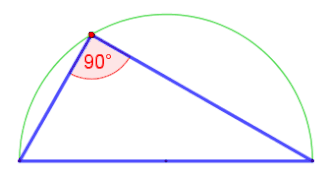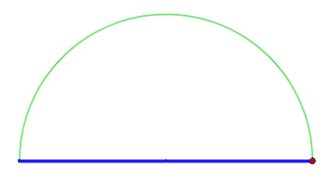
• Formulieren Sie den Satz des Thales in einer Skalarprodukt-Notation in einem Prähilbertraum und beweisen Sie den Satz. Starten Sie mit einem rechtwickligen Dreieck mit den Katheten $x,y\in V\setminus \{0_V\}$ mit $⟨x,y⟩=0$ und der Hypotenuse $x+y\in V\setminus \{0_V\}$.
• Formulieren Sie den Höhensatz in einer Skalarprodukt-Notation in einem Prähilbertraum und beweisen Sie den Satz. Starten Sie mit einem rechtwickligen Dreieck mit den Katheten $x,y\in V\setminus \{0_V\}$ mit $⟨x,y⟩=0$ und der Hypotenuse $x+y\in V\setminus \{0_V\}$.
  • Tragen Sie die Höhe $h$ und die Hypothenusenabschnitte $p,q$ ein.
  • Stellen Sie $x,y$ durch die Vektor $h,p,q$.
  • Welche Eigenschaften der Orthogonalität finden Sie in Ihrer Skizze.
• Welche Beweise für den Höhensatz in der Ebene kennen Sie? Können diese auf Prähilberträume analog übertragen werden?

Parallelogrammgleichung

Vektoren in der Parallelogrammgleichung

Für eine Skalarproduktnorm gilt zudem die Parallelogrammgleichung

$\Vert v+w{\Vert }^2+\Vert v-w{\Vert }^2=2(\Vert v{\Vert }^2+\Vert w{\Vert }^2)$

für alle Vektoren $v,w\in V$.

Satz von Jordan - von Neumann

Umgekehrt gilt nach dem Satz von Jordan-von Neumann: erfüllt eine Norm $\Vert \cdot \Vert$ die Parallelogrammgleichung, so ist sie von einem Skalarprodukt induziert. Dieses Resultat erhält man durch eine Polarisationsformel, bei reellen Vektorräumen zum Beispiel durch

$⟨v,w⟩=\frac{1}{4}(\Vert v+w{\Vert }^2-\Vert v-w{\Vert }^2)$.

Unitäre Invarianz

Eine Skalarproduktnorm ist weiterhin invariant unter unitären Transformationen. Ist $U:V\to W$ ein unitärer Operator (im endlichdimensionalen Fall eine unitäre bzw. orthogonale Matrix) von $V$ in einen weiteren Skalarproduktraum $W$ mit zugehöriger Norm, dann gilt

$\Vert Uv\Vert =\Vert v\Vert$,

Beweis für die Norminvaranz

Die Gleichung $\Vert Uv\Vert =\Vert v\Vert$ folgt unmittelbar aus der folgenden Gleichungskette:

$\Vert Uv{\Vert }^2=⟨Uv,Uv⟩=⟨U^{\ast }Uv,v⟩=⟨v,v⟩=\Vert v{\Vert }^2$

Dabei ist $U^{\ast }$ der zu $U$ adjungierte Operator. Im endlichdimensionalen Fall ist das dann die adjungierte bzw. transponierte Matrix).

Geometrischer Bezug

Eine Skalarproduktnorm ändert ihren Wert somit unter unitären Transformationen des Vektors nicht. Im reellen, endlichdimensionalen Fall sind solche Transformationen beispielsweise Drehungen des Vektors um den Nullpunkt.

Cauchy-Schwarz-Ungleichung

Eine Skalarproduktnorm erfüllt für alle Vektoren $v,w\in V$ die Cauchy-Schwarz-Ungleichung

$|⟨v,w⟩|\le \Vert v\Vert \Vert w\Vert$,

wobei Gleichheit genau dann gilt, wenn $v$ und $w$ linear abhängig sind.

Reeler Fall

Im reellen Fall können die Betragsstriche auch weglassen werden. Aus der Cauchy-Schwarz-Ungleichung folgt dann unmittelbar

$\frac{⟨v,w⟩}{\Vert v\Vert \Vert w\Vert }\le 1$,

Winkel zwischen Vektoren

Mit der obigen Ungleichung kann man den Winkel $\phi$ zwischen zwei reellen Vektoren über

$\cos (\phi )=\frac{⟨v,w⟩}{\Vert v\Vert \Vert w\Vert }$

definieren. Der Winkel $\phi$ liegt damit im Intervall $[0,\pi ]$, also zwischen $0^{\circ }$ und $180^{\circ }$. Für Winkel zwischen komplexen Vektoren gibt es eine Reihe unterschiedlicher Definitionen.

Orthogonalprojektion von Vektoren

Betrachtet man zwei verschiedene Vektoren $v,w\in V$, dann kann man die Orthogonalprojektion $P_w:V\to V$ von $v$ auf $w$ durch das Skalarprodukt ausdrücken:

$P_w(v)=\underset{=:\lambda }{\underbrace{\frac{⟨v,w⟩}{\Vert w{\Vert }^2}}}\cdot w$

Dabei liegt die Projektion von $P_w(v)$ in dem von $w$ aufgespannten eindimensionalen Unterraum von $V$

Aufgabe - Strahlensatz

Betrachten Sie die normierten Vektoren $v_1:=\frac{v}{\Vert v\Vert }$ und $w_1:=\frac{w}{\Vert w\Vert }$ mit $v=0_V=w$ als Vektoren auf dem Einheitskreis und betrachten Sie die

$\cos (\phi )=\frac{⟨v,w⟩}{\Vert v\Vert \Vert w\Vert }$

Aufgaben - Orthogonalprojektion

Betrachten Sie zunächst die Orthogonalprojektion von einem Vektor auf einen zweiten Vektor im ${ℝ}^1$.

Orthogonalprojektion

Aufgabe 1 - Orthogonalprojektion

Berechnen Sie die Orthogonalprojektion ${\overrightarrow{b}}_{\overrightarrow{a}}\in V\setminus \{0_V\}$ eines Vektors $\overrightarrow{b}\in V\setminus \{0_V\}$ auf einen Vektors $\overrightarrow{a}\in V\setminus \{0_V\}$ mit Hilfe des Skalarpdoktes U! Betrachten Sie dazu zunächst die Abbildung im ${ℝ}^2$ und wählen Sie im einfachen Fall die Vektoren $\overrightarrow{a}=(5,1)\in {ℝ}^2$ und $\overrightarrow{b}=(1,3)\in {ℝ}^2$. Berechnen Sie zunächst die Orthogonalprojekt ${\overrightarrow{b}}_{\overrightarrow{a}}$. Zeigen Sie, dass $\overrightarrow{a}=(5,1)\in {ℝ}^2$ und $\overrightarrow{b}-{\overrightarrow{b}}_{\overrightarrow{a}}\in {ℝ}^2$ senkrecht zueinander stehen.

Aufgabe 2 - Orthogonalprojektion

Übertragen Sie das Vorgehen aus dem ${ℝ}^2$ auf die stetigen Funktionen mit kompaktem Träger $[0,2\pi ]$ nach $ℂ$ und berechnen Sie die Orthogonalprojektion $g_f$ von $f$ auf $g$ für die beiden Vektoren $f,g\in V:=𝒞([0,2\pi ],ℂ)$ mit:

• $f(t):=2\cdot t+(i+1)\cdot t^3$
• $g(t):=t^2+it$

(Orthogonale Funkltion) Berechnen Sie zunächst die Orthonalprojektion $P_g(f)$ von $f$ auf $g$ und zeigen Sie, dass $f_0:=f-P_g(f)$ orthogonal orthogonal zu $g$! Berechnen Sie das Skalarprodukt $⟨g,f_o⟩$ mit:

$P_g(f)=\underset{=:\lambda }{\underbrace{\frac{⟨g,f⟩}{\Vert g{\Vert }^2}}}\cdot g$

Dabei liegt die Projektion von $P_g(f)$ in dem von $g$ aufgespannten eindimensionalen Unterraum von $V.$

(Normalisierung) Normalisieren Sie dann die beiden Vektoren $g$ zu $g_1$ und $f$ zu $f_o$, (also $\Vert g_1\Vert =\Vert f_1\Vert =1$) und mit $⟨f_1,g_1⟩=0$ gilt

Vorbemerkung zu Aufgabe 3

Andere Skalarprodukte kann man im reellen Fall durch jede symmetrische und positiv definite Matrix $M$ über

$⟨x,y{⟩}_{{}_M}=x^{T}My=⟨x,My⟩$

erzeugen. Dies ist auch im komplexen Fall durch jede positiv definite hermitesche Matrix $M$ über

$⟨x,y{⟩}_{{}_M}=\stackrel{T}{\stackrel{‾}{x}}My=⟨x,My⟩$

möglich.

Aufgabe 3 - Skalarprodukt mit vorgegebenen Eigenschaften

Geben Sie ein Skalarprodukt $⟨\cdot ,\cdot {⟩}_{{}_M}$ auf dem ${ℝ}^2$ an, bei dem die Vektoren $v:=(1,0)\in {ℝ}^2$ und $w:=(1,1)\in {ℝ}^2$ senkrecht aufeinander stehen - also $⟨v,w{⟩}_{{}_M}=0$ gilt. Verwenden Sie zunächst die folgende symmetrische Matrix für das gesuchte Skalarprodukt $⟨\cdot ,\cdot {⟩}_{{}_M}$:

$M=\left(\begin{array}{cc}{m}_1& m_2\\ m_2& m_3\end{array}\right)$

Satz des Pythagoras

Allgemein werden zwei Vektoren $v,w\in V$ orthogonal genannt, wenn ihr Skalarprodukt $⟨v,w⟩=0$ ist. Für orthogonale Vektoren gilt dann der Satz des Pythagoras für Skalarprodukträume

$\Vert v+w{\Vert }^2=\Vert v{\Vert }^2+\Vert w{\Vert }^2$.

Erweiterung von Pythagoras

Der Satz des Pythagoras kann auch auf eine endliche Summe paarweise orthogonaler Vektoren $v_1,\dots ,v_n\in V$ erweitert werden und es gilt dann

$\Vert v_1+\cdots +v_n{\Vert }^2=\Vert v_1{\Vert }^2+\cdots +\Vert v_n{\Vert }^2$.

Die entsprechende Erweiterung auf unendlich viele Summanden in einem Hilbertraum ist die Parsevalsche Gleichung (siehe auch Satz des Pythagoras).

Verallgemeinerung

Verzichtet man auf die positive Definitheit des Skalarprodukts, erhält man die folgende Verallgemeinerung. Jede positiv semidefinite hermitesche Sesquilinearform (im reellen Fall symmetrische Bilinearform) $(\cdot ,\cdot ):V\times V\to 𝕂$ induziert für $v\in V$ durch

$p(v)=\sqrt{(v,v)}$

eine Halbnorm.

Hausdorff-Eigenschaft - Trennung von Punkten

Mit dieser Halbnorm ist dann $(V,p)$ ein halbnormierter Raum, der aber im Allgemeinen kein metrischer Raum ist. Durch Restklassenbildung lässt sich aus einer Halbnorm aber eine zugehörige Norm ableiten und so erhält man wieder einen normierten Raum und damit auch einen metrischen und einen topologischen Raum.

Beispiel - Kovarianz

Die Kovarianz ist eine Bilinearform auf dem Raum der Zufallsvariablen mit endlichen zweiten Momenten, und wird zu einem Skalarprodukt auf dem Quotientenraum der Zufallsvariablen, die sich nur durch eine Konstante unterscheiden. Die von diesem Skalarprodukt induzierte Norm ist dann schlicht die Standardabweichung einer Zufallsvariablen.

Literatur

• Vorlage:Literatur
• Vorlage:Literatur
• Vorlage:Literatur
• Vorlage:Literatur

Siehe auch

• Semiskalarprodukt
• Satz des Thales
• Parallelogrammgleichung
• Kurs:Maßtheorie auf topologischen Räumen
• Kurs:Topologische Invertierbarkeitskriterien

Seiten-Information

Wiki2Reveal Foliensatz

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionalanalysis' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Funktionalanalysis/Skalarproduktnorm
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

Wikipedia2Wikiversity

Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:

• Skalarproduktnorm https://de.wikipedia.org/wiki/Skalarproduktnorm
• Datum: 28.1.2021 - Versionsgeschichte Wikipedia
• Wikipedia2Wikiversity-Konverter: https://niebert.github.com/Wikipedia2Wikiversity