Kurs:Maßtheorie auf topologischen Räumen/Wege in topologischen Räumen

Einführung

Wege in topologischen Räumen sollten die minimale Eigenschaft der Stetigkeit besitzen. Daher die folgende grundlegende Definition.

Definition - Weg in einem topologischen Raum

Sei $[a,b]\subset ℝ$ ein Interval und $(X,{𝒯}_X)$ topologischer Raum mit Topologie ${𝒯}_X$. Eine Abbildung:

$\gamma :[a,b]\to X$

heißt Weg in $X$, wenn die Abbildung $\gamma$ stetig ist. Das Intervall $[a,b]$ besitzt dabei Relativtopologie ${𝒯}_{[a,b]}$ der vom Betrag induzierten Topologie auf $ℝ$.

Bemerkung - Relativtopologie

Wenn $U\in {𝒯}_{ℝ}$ eine offene Menge in $ℝ$ ist, dann ist $U\cap [a,b]\in {𝒯}_{[a,b]}$ per Definition eine offene Menge in $[a,b]$ - also:

${𝒯}_{[a,b]}:=\{U_o\subset [a,b]:{\mathrm{\exists }}_{U\in {𝒯}_{ℝ}}:U_o=U\cap [a,b]\}$

Definition - Spur eines Weges

Sei $[a,b]\subset ℝ$ ein Interval und $(X,{𝒯}_X)$ topologischer Raum mit Topologie ${𝒯}_X$. Ferner sei ein Weg in $(X,{𝒯}_X)$ der

$\gamma :[a,b]\to X$

gegeben. Die Spur von $\gamma$ in $X$ bezeichnet dann die Menge aller Bildpunkte in $X$.

$Spur(\gamma ):=\{\gamma (t):t\in [a,b])\}$

Beispiel - Aufgabe

Wir betrachten nun den Vektorraum $(X,{𝒯}_X)$ der stetigen Funktionen $X:=𝒞(ℝ,ℝ)$. Die Topologie ${𝒯}_X$ wir dabei von einem System von Halbnormen erzeugt:

$\Vert f{\Vert }_n:=\underset{-n}{\overset{+n}{\int }}|f(x)|dx$

wird $(𝒞(ℝ,ℝ),\Vert \cdot {\Vert }_{\mathbb{N}}$ zu einem lokalkonvexen topologischen Vektorraum.

• Die Funktionen $f$ und $g$ mit $f(x)=x^2$ und $g(x):=cos(x)$ liegen in $X:=𝒞(ℝ,ℝ)$.
• Plotten Sie mit einen Schieberegeler $t\in [0,1]$ in Geogebra die Funktionen $\gamma (t):=(1-t)\cdot f+t\cdot g\in X$.

Animation für Weg in Funktionenräumen

Die folgende Animation zeigt mehrere Konvexkombinationen für $\gamma (t):=(1-t)\cdot f+t\cdot g\in X$ von zwei Funktionen $f$ und $g$ dar. Der rote Graph visualisiert den Weg von $f$ nach $g$ im Funktionenraum.

Konvexkombination von zwei Funktionen in Geogebra

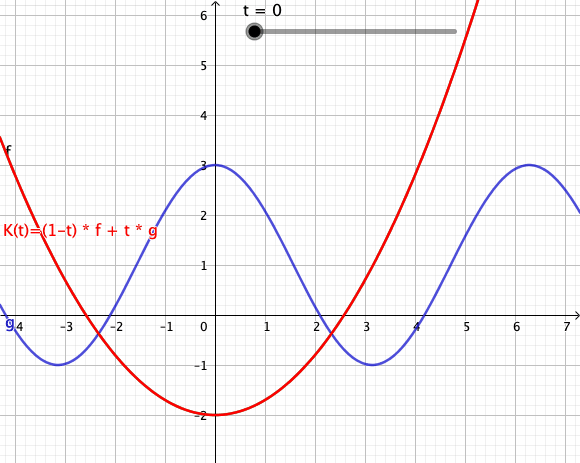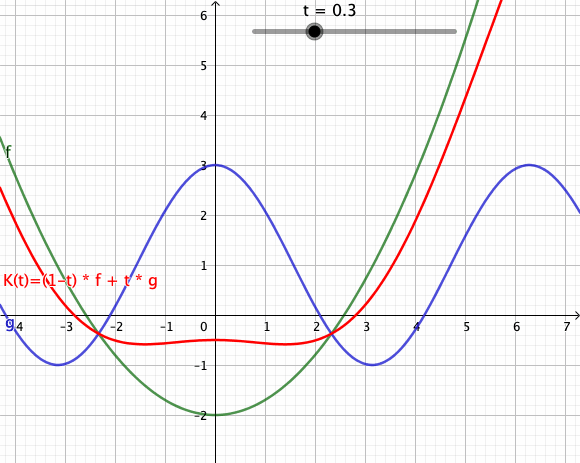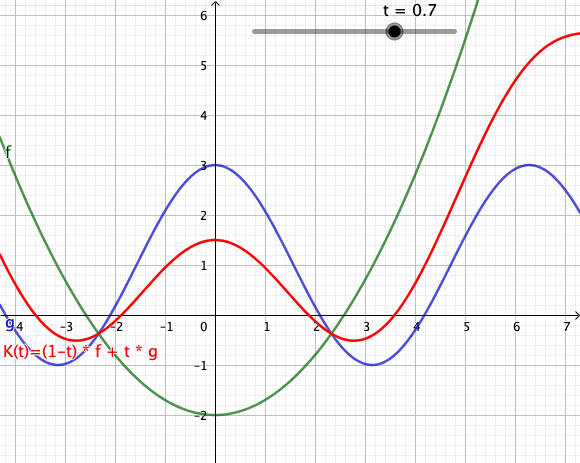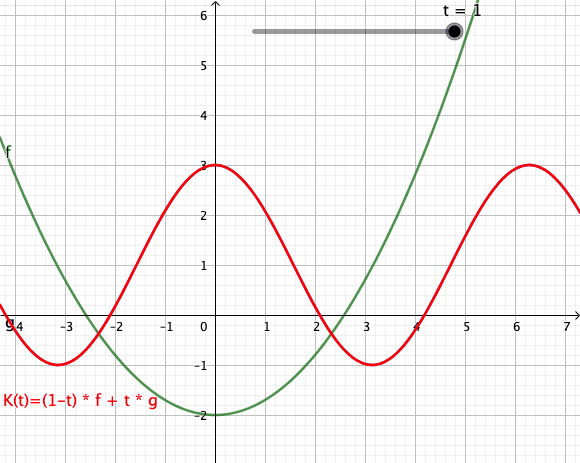
- Geogebra: Interaktives Applet - Download: Geogebra-File

Bemerkung - Bildpunkte der Spur

Die dargestellten Konvexkombinationen $\gamma (t)$ sind Bildpunkte in der Spur des Weges $\gamma (t):=(1-t)\cdot f+t\cdot g\in X$. Verwechseln Sie das bitte nicht mit dem Graph der dargestellten Funktion $\gamma (t)$ zum Zeitpunkt $t$. Die Animation als Ganzes ist eher mit einem Graphen eine Funktion zu vergleichen, bei der man Weg in dem Funktionenraum von $f$ nach $g$ beobachten kann.

Bemerkung - Weg in einem Funktionenraum

Berücksichtigen Sie dabei, dass $\gamma (t)=H_t$ eine Funktion ist, die Sie in Geogebra für einen Ausschnitt des Definitionsbereiches an der Stelle $x\in ℝ$ mit $\gamma (t)(x)=H_t(x)$ auswerten und den Gaph von $H_t$ in $t\in [a,b]$ darstellen

CAS4Wiki - Wege im dreidimensionalen Raum

Nutzen Sie nun den folgenden Link, der CAS4Wiki mit einer vordefinierten Kurve im ${ℝ}^3$ lädt und mit dem Bernsteinpolynom die Kurve im ${ℝ}^3$ in ${ℝ}^3$ plotten kann.

CAS4Wiki-Link für Kurven im ${ℝ}^3$

CAS4Wiki-Befehle

Der CAS4Wiki-Link enthält

• 4 vordefiniert Vektoren unter Variables,
• 2 vordefinierte Kurven im ${ℝ}^3$ mit den beiden Funktionen $cur(t)$ und der Konvexkombination mit dem Bernsteinpolynom, dass wie folgt definiert ist.

$$K(t):=v_1\cdot (1-t{)}^3+3v_2\cdot (1-t{)}^2\cdot t+3v_3\cdot (1-t)\cdot t^2+v_4\cdot t^3$$

Plotergebnis

Ausgeführt wird der ausgewählte Befehl mit dem Execute/Play-Button (Dreieck). Wenn man die jeweiligen Definitionen der Kurven auswählt erscheinen die folgenden beiden Plots.

Siehe auch

• Konvexkombination
• CAS4Wiki
• Wege in der komplexen Zahlenebene

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Maßtheorie auf topologischen Räumen' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Ma%C3%9Ftheorie%20auf%20topologischen%20R%C3%A4umen/Wege%20in%20topologischen%20R%C3%A4umen
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.