Kurs:Gewöhnliche Differentialgleichungen/4.0 Einführung

Runge-Kutta Verfahren

Runge-Kutta Verfahren (RKV) sind spezielle Einschrittverfahren, die durch ihre Struktur eine höhere Konsistenzordnung und damit eine höhere Genauigkeit der numerischen Lösung ermöglichen. Diese Verfahren wurden vom deutschen Mathematiker Wilhelm Kutta 1901 auf Basis eines Artikels von Carl Runge aus dem Jahre 1895 entwickelt.

Betrachten wir die Gleichung $y^{\prime }(t)=f(t,y(t))$, so wird die höhere Konsistenzordnung der Runge-Kutta-Verfahren durch die höhere Anzahl von Funktionsauswertungen der Funktion $f$ (rechte Seite der Gleichung) an den Stellen zwischen $t_i$ und $t_{i+1}=t_i+h$ erreicht. Die Zwischenstellen $t_i+ch$ nennen wir Stufen, oder Stützstellen, wobei $c\in [0,1]$ und $h$ die Schrittweite ist.

In den bislang studierten ESV, wie das Eulerverfahren, Trapezregel, Mittelpunktregel (in expliziter oder impliziter Form), wurde in jedem Schritt ein bis zwei Auswertungen von $f$ an den Stellen $t_i,t_{i+1/2}$ oder $t_{i+1}$ verwendet. In den RKV wird die Anzahl der Stützstellen erhöht und ihre Lage entsprechend bestimmt, damit eine möglichst hohe Konsistenzordnung erreicht werden kann. Die bisher bekannten ESV können als die einfachsten Runge-Kutta Verfahren einordnet werden.

---

Definition 4.1 (Runge-Kutta Verfahren).

Sei $s\in \mathbb{N}$ die Anzahl von Stufen/Stützstellen, $A\in {ℝ}^{s\times s}$ die Koeffizientenmatrix mit Einträgen $(A{)}_{j,m}=:a_{jm}$, sei $\overrightarrow{b}\in {ℝ}^s$ Vektor der Gewichte und $\overrightarrow{c}\in {ℝ}^s$ Vektor der Stützstellen.
Das Verfahren mit der Vorschrift $$\begin{array}{cc}{\eta }_0& =y_0,\\ k_j& =f(t_i+h{c}_j,{\eta }_i+h\sum _{m=1}^s{a}_{jm}{k}_m)\text{für}j=1,\dots ,s,(4.1)\\ {\eta }_{i+1}& ={\eta }_i+h\sum _{j=1}^s{k}_j{b}_j\text{für}i=0,1,\dots ,N_h-1\end{array}(4.2)$$ heißt s-stufiges Runge-Kutta Verfahren.

---

Die Runge-Kutta Verfahren können schematisch auch im sog. Butcher-Tableau angegeben werden:

oder kurz

$\overrightarrow{c}=\left(\begin{array}{c}{c}_1\\ ⋮\\ c_s\end{array}\right),{\overrightarrow{b}}^T=(b_1,\dots b_s)$.

Beispiel 4.1.

Die Funktionsauswertung $k_j$ eines RKV für $j=2$ ist $k_2=f((t_i+h{c}_2,{\eta }_i+h\sum _{m=1}^s{a}_{2m}{k}_m)=f((t_i+h{c}_2,{\eta }_i+h{\overrightarrow{a}}_2\cdot \overrightarrow{k}),$ wobei ${\overrightarrow{a}}_2=(a_{21},\dots ,a_{2s})$ die zweite Zeile der Matrix $A$ ist und ${\overrightarrow{k}}_2=(k_1,\dots ,k_s)$ $\diamond .$

Der neue Wert der numerischen Lösung nach einem Schritt des RKV (auch Runge-Kutta Update genannt) berechnet sich nach (4.2) als ${\eta }_{i+1}={\eta }_i+h\sum _{j=1}^s{k}_j{b}_j.$ Der Vergleich dieser Gleichung mit der Volterra’schen Integralgleichung (2.1) auf dem Intervall $(t_i,t_{i+1})$, $y(t_i+h)=y(t_i)+\underset{t_i}{\overset{t_{i+1}}{\int }}f(s,y(s))ds$ führt zu folgenden Überlegungen: Ersetzt man das Integral ${\int }_{t_i}^{t_{i+1}}f(s,y(s))ds$ sinnvol durch eine Summe, sodass $h\sum _{j=1}^s{k}_j{b}_j\approx \underset{t_i}{\overset{t_{i+1}}{\int }}f(s,y(s))ds,$ so wird eine Quadratur von $f$ angewendet, um den neuen Wert ${\eta }_{i+1}$ zu berechnen. Dabei sind $k_j$ die $s$ Knoten dieser Quadratur an den Stützstellen $t_i+h{c}_j$ (vergleiche (4.1)) und $b_j$ die Gewichte der Quadratur. Ein RKV zu konstruieren bedeutet daher, eine geeignete Quadratur des Integrals ${\int }_{t_i}^{t_{i+1}}f$ zu finden. Bei den einfachsten RKV (dabei handelt es sich um die im 3. Kapitel vorgestellten Einschrittverfahren) handelt es sich um die Anwendung von Quadraturen, wie beispielsweise die Rechteck-, Mittelpunkt- und Trapezregel für das Integral ${\int }_{t_i}^{t_{i+1}}f(s,y(s))ds$ (siehe Bemerkung 3.1 Punkt iii) und Abbildungen 3.1, 3.2, 3.3, 3.4). Das Butcher-Tableau kann wie folgt interpretiert werden: Der Vektor $\overrightarrow{c}$ beschreibt die Stützstellen und der Vektor $\overrightarrow{b}$ die Gewichte der zugehörigen Quadratur von $f$ auf dem Intervall $(t_i,t_{i+1})$. Die Matrix $A$ spiegelt in gewissem Sinne die Differentialgleichung zurück. Dies kann wie folgt begründet werden:
Nach der Definition der Runge-Kutta Verfahren, siehe (4.1), und mithilfe der Differentiagleichung $y^{\prime }=f(t,y)$ kann darauf geschlossen werden, dass die $k_j$ die Ableitungen der gesuchten Funktion an den Stützstellen $t_i+h{c}_j$ approximieren, sodass mit $j=1,\dots s$ und $i$ - fest, $$k_j\approx y^{\prime }(t_i+h{c}_j)$$

gilt. Da die Matrix $A$ zur Berechnung von $k_j$ dient, spiegelt diese automatisch die Differentialgleichung in oben beschriebenem Sinne zurück.

Anhand der Matrix $A$ kann zwischen expliziten und impliziten RK- Verfahren unterscheiden werden:

• Explizite Runge-Kutta Verfahren (eRKV):
  

Ist die Matrix $A$ eine untere Dreiecksmatrix, handelt es sich um explizite RKV. Hierbei werden in jedem Schrit $t_i$ für die Berechnung von $k_j,j=1,\dots s$ immer nur die vorher berechneten $k_1,\dots ,k_{j-1}$ verwendet. In diesem Fall kann man $k_j$ durch das Einsetzen explizit berechnen als $$k_j=f(t_i+h{c}_j,{\eta }_i+h\sum _{m=1}^{j-1}{a}_{jm}{k}_m).$$

• Implizite Runge-Kutta Verfahren (iRKV):
  

Ist die Matrix $A$ eine voll besetzte Matrix, so hängen $k_j$ für jedes $j=1,\dots s$ im Allgemeinem von allen $k_1,\dots ,k_s$ ab. Die Berechnung von $k_j$ erfolgt dann durch die Lösung eines (linearen oder ggf. nichlinearen) Systems von Gleichungen. In diesem Fall ist die Berechnung von $k_j$ einfacher oder kostengünstiger, wenn $A$ eine Dreiecksmatrix ist. Man unterscheidet in diesem Fall zwischen:

• • DIRK-Verfahren: ’diagonal implizit RK -Verfahren’:
    

Matrix $A$ ist eine Dreiecksmatrix mit $diag(A)\ne \mathrm{𝟎}$,

• • SDIRK-Verfahren: ’simply diagonal implizit RK -Verfahren’:
    

Matrix $A$ ist eine Dreiecksmatrix mit $diag(A)=\lambda diag(I)\ne \mathrm{𝟎},\lambda \in ℝ,I$ ist eine Einheitsmatrix,

• • SIRK-Verfahren ’simply implizit RK -Verfahren’:
    

Matrix $A$ ist eine vollbesetzte Matrix, wobei $diag(A)=\lambda diag(I)$ und die obere Dreiecksmatrix besteht auch aus $\lambda$’s.

Nun geben wir einige konkrete Beispiele von Runge-Kutta Verfahren an:
Explizites Eulerverfahren, $s=1$:

$$\begin{array}{c}\\ k_1& =f(t_i+0.h,{\eta }_i+0.h{k}_1)=f(t_i,{\eta }_i)\\ {\eta }_{i+1}& ={\eta }_i+h{k}_1\equiv {\eta }_i+hf\underset{=k_1}{\underbrace{(t_i,{\eta }_i)}}\end{array}$$
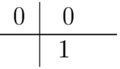
Implizites Eulerverfahren, $s=1$:

$$\begin{array}{c}\\ k_1& =f(t_i+1.h,{\eta }_i+1.h{k}_1)\\ {\eta }_{i+1}& ={\eta }_i+h{k}_1\equiv \mathrm{\%}{\eta }_i+hf\underset{=k_1}{\underbrace{(t_i+h,{\eta }_i+h{k}_1)}}={\eta }_i+hf(t_i+h,\underset{={\eta }_{i+1}}{\underbrace{{\eta }_i+h{k}_1}})\end{array}$$
Verbessertes Eulerverfahren (explizite Mittelpunktregel), $s=2$:

$$\begin{array}{cc}{k}_1& =f(t_i,{\eta }_i)\\ k_2& =f(t_i+\frac{h}{2},{\eta }_i+\frac{h}{2}{k}_1)\\ {\eta }_{i+1}& ={\eta }_i+h(0.k_1+1.k_2)\\ & \equiv {\eta }_i+hf\underset{=k_2}{\underbrace{(t_i+\frac{h}{2},{\eta }_i+\frac{h}{2}\underset{=k_1}{\underbrace{f(t_i,{\eta }_i)}})}}\end{array}$$

Klassisches Runge-Kutta Verfahren, $s=4$:

$$\begin{array}{cc}{k}_1& =f(t_i,{\eta }_i)\\ k_2& =f(t_i+\frac{h}{2},{\eta }_i+\frac{h}{2}{k}_1)\\ k_3& =f(t_i+\frac{1}{2}h,{\eta }_i+\frac{h}{2}{k}_2)\\ k_4& =f(t_i+h,{\eta }_i+h{k}_3)\\ {\eta }_{i+1}& ={\eta }_i+h(\frac{k_1}{6}+\frac{k_2}{3}+\frac{k_3}{3}+\frac{k_4}{6})\end{array}$$

$3/8$- Regel, $s=4$:

$$\begin{array}{cc}{k}_1& =f(t_i,{\eta }_i)\\ k_2& =f(t_i+\frac{h}{3},{\eta }_i+\frac{h}{3}{k}_1)\\ k_3& =f(t_i+\frac{2}{3}h,{\eta }_i-\frac{h}{3}{k}_1+h{k}_2)\\ k_4& =f(t_i+h,{\eta }_i+h{k}_1-h{k}_2+h{k}_3)\\ {\eta }_{i+1}& ={\eta }_i+h(\frac{k_1}{8}+\frac{3}{8}{k}_2+\frac{3}{8}{k}_3+\frac{k_4}{8})\end{array}$$

Zwei weitere explizite 3-stufige RKV sind durch folgende Butcher-Tableaus gegeben:

Verfahren von Heun, $s=3$ (1900): $$3-stufiges eRKV