Kurs:Funktionentheorie/Wege

Definition: Weg

Gegeben sei eine Teilmenge $U\subset ℂ$. Ein Weg in $U$ ist eine stetige Abbildung mit

$\gamma :[a,b]\to U$ mit $a<b$ und $a,b\in ℝ$.

Definition: Spur eine Weges

Die Spur eines Weges $\gamma :[a,b]\to U$ in $U\subset ℂ$ ist das Bild der Funktion $\gamma$.

$\mathrm{S}\mathrm{p}\mathrm{u}\mathrm{r}(\gamma ):=\{\gamma (t)\in ℂ|t\in [a,b]\}$

Definition: Geschlossener Weg

Gegeben sei ein Weg $\gamma :[a,b]\to U$ in $U\subset ℂ$. Die Abbildung $\gamma$ heißt geschlossener Weg wenn gilt:

$\gamma (a)=\gamma (b)$

Definition: Bereich

Sei $U\subset ℂ$ eine offene Teilmenge $ℂ$. Dann nennt man $U$ Bereich.

Definition: wegzusammenhängend

Sei $U\subset ℂ$ eine nicht-leere Menge.

$U$ wegzusammenhängend $:⟺{\mathrm{\forall }}_{z_1,z_2\in U}{\mathrm{\exists }}_{\gamma :[a,b]\to U}:\gamma (a)=z_1\wedge \gamma (b)=z_2\wedge Spur(\gamma )\subseteq U$

Definition: Gebiet

Sei $G\subset ℂ$ eine nicht-leere Teilmenge $ℂ$. Ist

• $G$ offen
• $G$ wegzusammenhängend

Dann nennt man $G$ ein Gebiet $ℂ$.

Beispiel (Kreiswege)

Es seien $z_o\in ℂ$ und eine komplexe Zahl und $r>0$ als Radius gegeben. Dazu definiert man einen Kreisweg ${\gamma }_{z_o,r}:[0,2\pi ]\to ℂ$ um $z_o\in ℂ$ als:

${\gamma }_{z_o,r}(t):=z_o+r\cdot e^{i\cdot t}$

Beispiel - Wege mit Ellipse als Spur

Es seien $z_o\in ℂ$ und eine komplexe Zahl und $a,b>0$ als Halbachsen einer Ellipse gegeben. Dazu definiert man einen elliptischen Weg ${\gamma }_{z_o,a,b}:[0,2\pi ]\to ℂ$ um $z_o\in ℂ$ als:

${\gamma }_{z_o,a,b}(t):=z_o+a\cdot \cos (t)+i\cdot b\cdot \sin (t)$

Gärtnerkonstruktion einer Ellipse

Konvexkombinationen

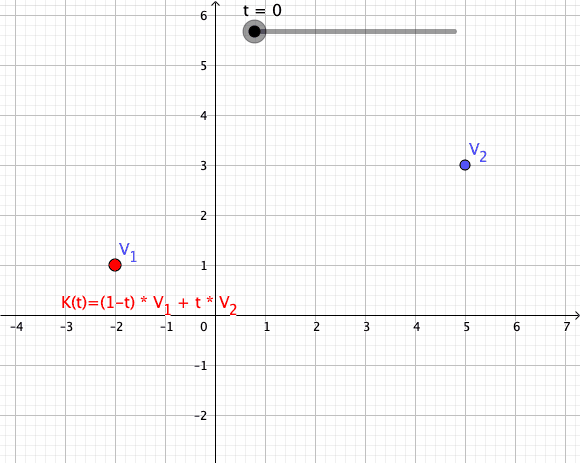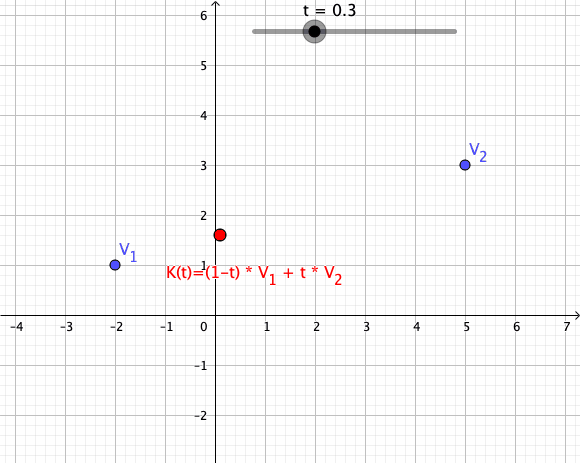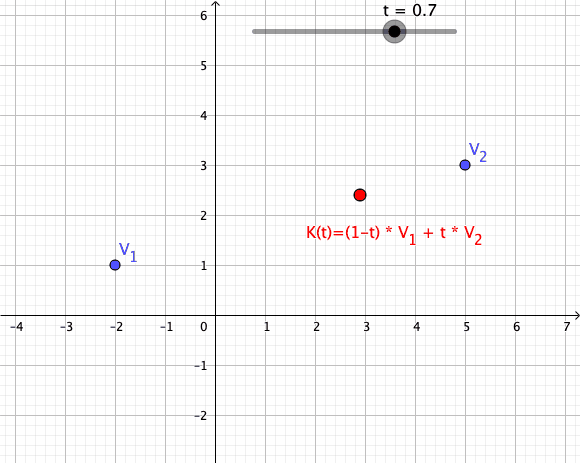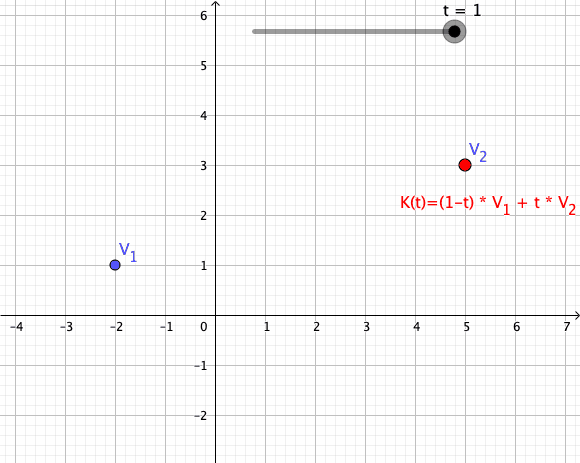
Es seien $z_1,z_2\in ℂ$ komplexe Zahlen und $t\in [0,1]$ als Skalar gegeben. Damit definiert man einen Weg ${\gamma }_{z_1,z_2}:[0,1]\to ℂ$, der die Verbindungsstrecke zwischen $z_1,z_2\in ℂ$ als Spur beinhaltet:

${\gamma }_{z_1,z2}(t):=(1-t)\cdot z_1+t\cdot z_2$

Einen solchen Weg nennt man Konvexkombination 1. Ordnung (siehe auch Konvexkominationen höherer Ordung)

Animation einer Konvexkombination von zwei Vektoren als Abbildung

Konvexkombination als Abbildung in einer GIF-Animation

Integrationweg

Gegeben sei ein Gebiet $G\subset ℂ$. Ein Integrationsweg in $G$ ist ein Weg, der stückweise stetig differenzierbar ist mit

$\gamma :[a,b]\to U$ mit $a<b$ und $a,b\in ℝ$.

Bemerkung

Ein Integrationweg kann z.B. durch stückweise durch Konvexkombinationen zwischen mehreren Punkten $z_1,\dots z_n\in ℂ$ ausgedrückt werden. Der gesamte Weg damit insbesondere an den Punkten $z_1,\dots z_n\in ℂ$ nicht notwendig differzierbar. Die Spur eines solchen Weges nennt man auch Polygonzug.

Siehe auch

• Ellipse
• Konvexkombination
• Wege in topologischen Vektorräumen

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionentheorie' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Wege
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.