Kryptologie - Mathematische Vertiefung (PH Freiburg SS 2017)

Auf diesen Seiten entsteht gemeinsam mit Studierenden der PH Freiburg eine Sammlung zu Inhalten der Kryptologie, die mathematisch vertieft werden und für den Einsatz im Unterricht der Sekundarstufe I aufbereitet werden. In der Lehrveranstaltung soll der mathematische Horizont, auch über die mit dem Schulcurriculum verbundene Mathematik hinaus erweitert werden. (Dozentin: Dr. Melanie Platz)
Hilfe für die Bearbeitung des Wikis: Wikipedia-Hilfe und für das Einfügen mathematischer Formeln: Tex-Hilfe

Die Kryptologie lässt sich in die Kryptographie und die Kryptoanalyse gliedern.
Die Kryptographie bezeichnet die Wissenschaft der Entwicklung von Kryptosystemen und die Kryptoanalyse die Kunst diese zu brechen.


Definition: Text/ Nachricht $A$ ist ein Alphabet.
$A^n=A\times A\times ...\times A=\{(z_1,...,z_n)\mid \mathrm{\forall }k\in \{1,...,n\}:z_k\in A\}$ ist das $n$-fache kartesische Produkt des Alphabets $A$
$A^n$ sind die Nachrichtentexte der Länge $n$.
$A^{+}=\bigcup _{n=1}^{\mathrm{\infty }}{A}^n$
$A^{+}$ sind alle Nachrichten aus Buchstaben des Alphabets $A$.

Definition: Bijektiver Schlüssel
$A,B$ sind Alphabete. $f:A\to B$ ist eine bijektive Abbildung.
Dann nennt man $f$ einen bijektiven Schlüssel für Nachrichten aus $A^{+}$.

Bijektivität

Arbeitsauftrag 1 a): Was war nochmal „bijektiv“? Erläutern Sie den Begriff mathematisch mit Beispielen und stellen Sie dar, wie Sie den Begriff Schüler*innen der Sekundarstufe I erklären würden.

Beispiel für eine bijektive Funktion

Definition: Bijektivität
Jedem Element x aus der Wertemenge A wird genau ein Element y aus der Zielmenge B zugeordnet.

Ist eine Abbildung surjektiv (jedem Element x aus der Wertemenge A wird mindestens ein Element y aus der Zielmenge B zugeordnet) und injektiv (jedem Element x aus der Wertemenge wird höchstens ein Element y aus der Zielmenge zugeordnet), dann ist sie bijektiv. Bijektive Abbildungen sind immer umkehrbar.

Beispiel für eine bijektive Funktion

Erklärung für Schüler: Beispiel aus dem Alltag

• "In einem Glas befinden sich 25 Bonbons. Die Klasse besteht aus 25 Schülerinnen und Schülern. Jeder Schüler bekommt genau ein Bonbon."
  Diese Abbildung ist bijektiv, da ja jeder Schüler genau ein Bonbon bekommt. Niemand bekommt mehrere Bonbons und auch niemand wird ausgelassen.
  
• "Zum Frühstück liebt Familie Maier Brezeln. Jedes Familienmitglied isst immer mindestens eine Brezel. Der Vater isst immer zwei Brezeln und Pit und Anna manchmal auch, wenn sie besonders großen Hunger haben."
  Diese Situation ist nicht bijektiv, da nicht jeder genau eine Brezel isst.
• "Jeder Mensch muss einmal sterben"
  Diese Situation ist bijektiv, weil wirklich jeder Mensch einmal sterben wird und man stirbt nur einmal.
  

Definition: Abbildung

Es seien zwei Mengen $A,B$ gegeben. Unter einer Abbildung $f$ von $A$ nach $B$ verstehen wir eine Vorschrift, die jedem Element $x\in A$ genau ein Element $y=f(x)\in B$ zuordnet:
$\mathrm{\forall }x\in A\mathrm{\exists }!y\in B:y=f(x)$

Definition: Injektivität, Surjektivität, Bijektivität

Es seien A und B Mengen und $f:A\to B$ eine Abbildung zwischen A und B.
f heißt:

• injektiv$:\iff \mathrm{\forall }{a}_1,a_2\in A:f(a_1)=f(a_2)\to a_1=a_2$.
• surjektiv$:\iff \mathrm{\forall }b\in B\mathrm{\exists }a\in A:f(a)=b$.
• bijektiv$:\iff f$ ist injektiv und $f$ ist surjektiv.

Symmetrische Verschlüsselung

Definition: Symmetrische Verschlüsselung
Sender und Empfänger haben den gleichen Schlüssel.

Substitutionsalgorithmen

Bei einem Substitutionsalgorithmus oder Verschiebechiffre behält jeder Buchstabe seine Position, wird aber durch einen anderen ersetzt.

Monoaplhabetische Substitution

Als monoalphabetische Substitution bezeichnet man ein Verschlüsselungsverfahren, bei dem nur ein einziges (festes) Schlüsselalphabet zur Verschlüsselung, also zur Umwandlung des Klartextes in den Geheimtext, verwendet wird. Es gibt genau 26! monoalphabetische Chiffrierungen über dem natürlichen Alphabet $\{a,...,z\}$.
Die Caesar-Verschlüsselung ist ein Sonderfall der einfachen monoalphabetischen Substitution.

Caesar-Verschlüsselung

Arbeitsauftrag 1 b): Wie Funktioniert die „Caesar-Verschlüsselung“? Erläutern Sie die Funktionsweise, die mathematischen Hintergründe und erstellen Sie mit Hilfe von LibreOffice Calc (oder Microsoft Excel) ein Programm, mit dem das Ver- und Entschlüsseln mittels Caesar-Verschlüsselung möglich ist.

Excel Graph der Funktion von Klartext auf Chiffrierter Text

Die "Caesar-Verschlüsselung" ist eine Verschlüsselungstechnik, bei dem jeder Buchstabe um die gleiche Zahl verschoben und so einem anderen Buchstaben zugeordnet wird. Bei einer Verschiebung v um 3 wird z.B. A zu D chiffriert, B zu E, C zu F, usw. Dabei handelt es sich um eine zyklische Verschiebung, das bedeutet: Bei einer Verschiebung um 3 wird X zu A, Y zu B und Z zu C. Dabei wird der gesamte Klartext um die gleiche Zahl verschoben. Die Caesar-Verschlüsselung bietet eine begrenzte Anzahl an Verschlüsselungsmöglichkeiten.

Mathematischer Hintergrund: Gegeben ist ein Klartextalphabet $A=\{z_1,z_2,...,z_{|A|}\}$ und ein Geheimtextalphabet $B$ und es gilt $A=B$. Die Mächtigkeit $|A|$ ist die Anzahl aller Elemente des Alphabets $A$. Man nummeriert jedes Element des Alphabets mit den natürlichen Zahlen von $0$ bis $|A|-1$ mit Hilfe folgender Abbildung:
$f:A\to \{0,...,|A|-1\}$

$z_1\mapsto 0$

$z_2\mapsto 1$

$⋮$

$z_{|A|}\mapsto |A|-1$

Bei der Caesar-Verschlüsselung handelt es sich um eine bijektive Abbildung
$V:A\to B$

$a\mapsto V(f(a))=(f(a)+k)mod|A|$,

wobei $k\in \mathbb{N},0\le k\le |A|$ der Schlüssel ist.
Entschlüsselt wird mit der Umkehrabbildung von $V,V^{-1}=:E$.
$E:B\to A$

$b\mapsto E(f(b))=(f(b)-k)mod|A|$,

wobei k derselbe Schlüssel ist, der zum Verschlüsseln verwendet wurde.

Transpositionschiffre

Bei einer Transpositionschiffre bleiben die Buchstaben was sie sind, aber nicht wo sie sind. Es handelt sich um eine Permutation der Stellen des Klartextes.

Skytala-Verschlüsselung

Arbeitsauftrag 1 c): Wie Funktioniert die „Skytala-Verschlüsselung“? Erläutern Sie die Funktionsweise, die mathematischen Hintergründe und erstellen Sie mit Hilfe von LibreOffice Calc (oder Microsoft Excel) ein Programm, mit dem das Ver- und Entschlüsseln mittels Skytala- Verschlüsselung möglich ist.

Bei der Entschlüsselung einer Skytala-Verschlüsselung wird ein horizontal beschrifteter Textstreifen um einen Stab gewickelt. Dadurch wird der codiert aufgeschriebene Text wieder lesbar. Bei der Verschlüsselung wird die Skytala-Verschlüsselung variiert mit dem Durchmessers des verwendeten Stabes. Die Abstände im resultierenden Textband, zwischen zwei Zeichen aus dem zu verschlüssenden Text, sind direkt abhängig vom verwendeten Stab. Diese Abstände bleiben im kompletten Textband gleich. Zeilenweise lässt sich dann auf dem Stab der ursprüngliche Text wieder lesen.

Mathematischer Hintergrund: Gegeben ist ein Klartext mit der Textlänge $t$. Die Positionen der Buchstaben sind bei Transpositionschiffren wichtig, die Positionen im Klartext stammen aus der Menge $P:=\{1,...,t\}$ und sind folgendermaßen nummeriert: $(1,2,...t)$. Sei nun $u$ der Umfang des Stabs, der durch die Anzahl der Zeilen des Geheimtextes bestimmt wird und $l$ die Länge der Nachricht, wenn sie um den Stab gewickelt ist, die durch die Anzahl der Spalten des Geheimtextes bestimmt wird. Es gilt $t=l\cdot u$ Dann wird durch folgende Abbildung verschlüsselt:
$V:P\to P$

$p\mapsto \{\begin{array}{c}(p-1)l+1,falls0<p\le u,\\ (p-u-1)l+2,fallsu<p\le 2u,\\ ⋮\\ (p-(l-1)u-1)l+l,falls(l-1)u<p\le lu.\end{array}$

Entschlüsselt wird wiederum mit der Umkehrabbildung $V^{-1}$.

Gartenzaun-Chiffre

Arbeitsauftrag 1 d): Wie Funktioniert die „Gartenzaun-Verschlüsselung“? Erläutern Sie die Funktionsweise, die mathematischen Hintergründe und erstellen Sie mit Hilfe von LibreOffice Calc (oder Microsoft Excel) ein Programm, mit dem das Ver- und Entschlüsseln mittels Gartenzaun-Verschlüsselung möglich ist.

Auch bei der Gartenzaunchiffre ist das Ziel, einen Klartext in eine Geheimbotschaft umzuwandeln, die mit einem Schlüssel wieder dechiffriert werden kann.

Verschlüsselung

Abbildung Gartenzaunchiffre

Bei der Verschlüsselung wird mithilfe dieser Methode der Klartext in einem Zickzack-Muster aufgeschrieben (siehe Abb.). Dabei sind folgende Kriterien entscheidend:

• Die Höhe des Gartenzauns, diese entspricht der Anzahl der Zeilen des Zickzack-Musters
• Der Beginn des Gartenzauns->Es ist möglich, dass der Gartenzaun nicht auf der obersten Stufe beginnt
• Die Richtung des Gartenzaunes->Der Gartenzaun kann von rechts nach links bzw. auch von links nach rechts aufgestellt werden.
• Zusätzlich können die Stufen beim weiteren Verschlüsseln vertauscht werden.

Zuerst bestimmt der Verschlüssler die Höhe des Gartenzauns und schreibt den Klartext in dem Zickzack-Muster auf. Dabei überlegt er sich, in welcher Zeile er beginnt und in welcher Richtung er das Zickzack-Muster notiert. Um die Methode noch sicherer zu machen, vertauscht er die Zeilen, wenn er die Buchstaben aus dem Zickzack-Muster zeilenweise abschreibt. Er beginnt dann nicht mit der ersten, sondern z. B. mit der dritten Zeile und schreibt die Buchstaben hintereinander gesondert auf, dann folgt die erste Zeile usw. Damit der Entschlüssler weiß, welche dieser Kriterien der Verschlüssler benutzt hat, braucht dieser einen separaten Schlüssel, den ihm der Verschlüssler zusätzlich mitteilen muss.

Schlüsselerzeugung:

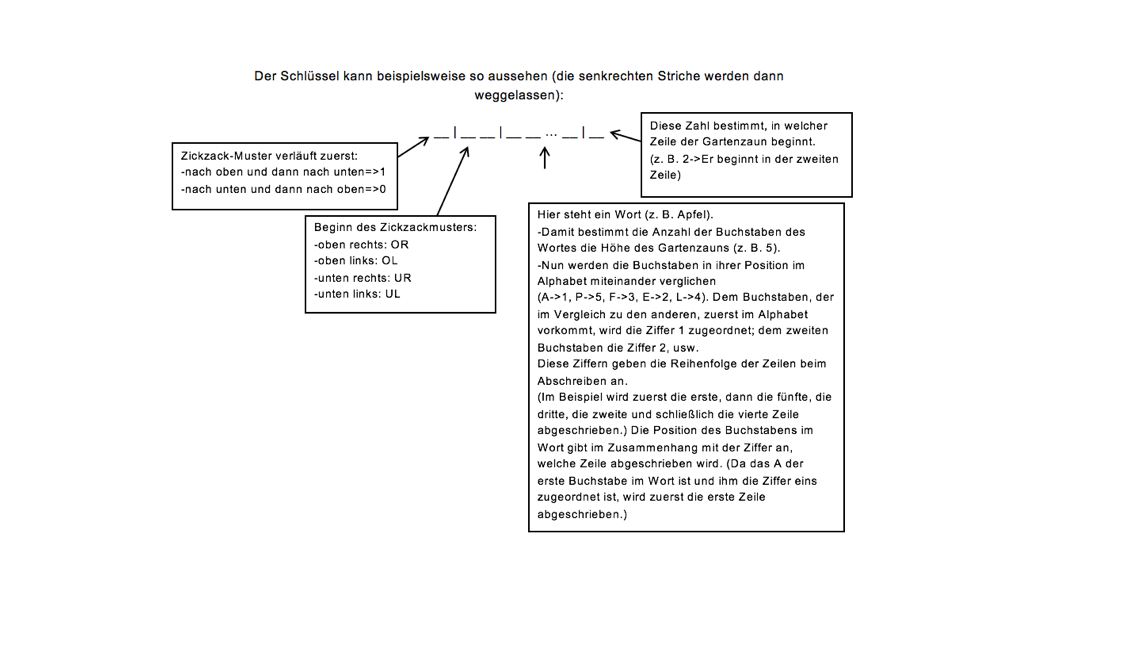
Entschlüsselung

Für die Entschlüsselung ist es wichtig, dass die Person, die die Nachricht entschlüsseln möchte bzw. für die die Geheimbotschaft bestimmt ist, über den vom Verschlüssler individuell gesetzten Schlüssel Bescheid weiß. Die Vorgehensweise kann bei der Entschlüsselung unterschiedlich verlaufen. Wird davon ausgegangen, dass der oben in der Abbildung veranschaulichte Schlüssel gewählt wurde, bietet es sich beispielsweise an folgendermaßen beim Entschlüsseln vorzugehen:

1. Es werden die einzelnen Zeilen je nach Zeilenhöhe des Gartenzauns untereinander nummeriert.

2. Unter jeden Buchstaben des Worts in der dritten Spalte werden Ziffern je nach alphabetischer Reihenfolge der Buchstaben unter die einzelnen Buchstaben des Worts (hier: APFEL) geschrieben.

3. Mithilfe der zweiten sowie der letzten Spalte ist es nun möglich, den Beginn des ersten Buchstabens der Botschaft zu ermitteln.

4. Je nach Verlauf des Zickzack-Musters, welches sich aus der ersten Spalte ablesen lässt, kann nun die Nachricht unter Beachtung der vertauschten Stufen im Zickzack-Muster über die Stufen verteilt von links nach rechts aufgeschrieben werden.

Mathematischer Hintergrund: Gegeben ist ein Klartext mit der Textlänge $t$. Die Positionen der Buchstaben sind bei Transpositionschiffren wichtig, die Positionen im Klartext stammen aus der Menge $P:=\{1,...,t\}$ und sind folgendermaßen nummeriert (wir legen fest, dass unser Gartenzaun mit variabler Höhe $h$ und Anzahl der Spitzen $m$ und Täler $m-1$ mit $h,m\in \mathbb{N}$ stets folgende Form hat):

Form des Gartenzauns

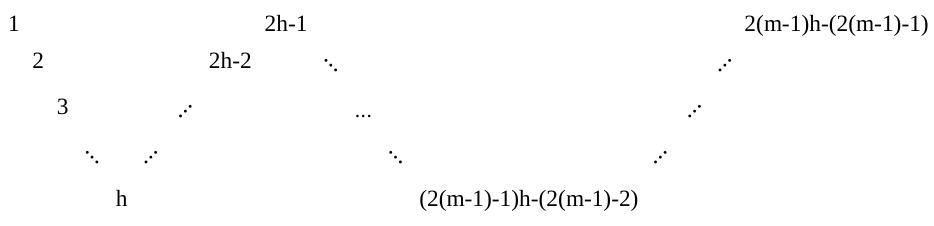
Dann wird durch folgende Abbildung verschlüsselt:
$V:P\to P$

$p\mapsto \{\begin{array}{c}2(p-1)h-(2(p-1)-1),falls0<p\le m,\\ ⋮\\ (2(p-1)-1)h-(2(p-1)-2),fallsm+(h-2)(m-1)<p\le m(h-2)(m-1)+(m-1).\end{array}$

Entschlüsselt wird wiederum mit der Umkehrabbildung $V^{-1}$.

Kryptoanalyse

Systematische Schlüsselsuche

Jeder Verschlüsselungsalgorithmus kann durch eine systematische Anwendung möglicher Schlüssel auf den Geheimtext gebrochen werden. Bei einer Anzahl von $k$ möglichen Schlüsseln, benötigt man höchstens $k$ Versuche, durchschnittlich allerdings nur $\frac{k}{2}$ Versuche. Je größer die Anzahl der möglichen Schlüssel, umso schwerer ist ein Verschlüsselungsalgorithmus zu knacken.

Statistische Analyse

Die Statistische Analyse kann bei Substitutionsalgorithmen angewendet werden. Durch die Bestimmung der relativen Häufigkeiten der Buchstaben eines Geheimtextes (z.B. mit Hilfe eines Applets zum Buchstabenzählen), können diese mit der Häufigkeit der Buchstaben der deutschen Sprache abgeglichen werden und entsprechend ersetzt werden.

Unterrichtsplanung

Arbeitsauftrag 1 e): Wie würden Sie Caesar-Verschlüsselung, Skytala-Verschlüsselung und Gartenzaun- Chiffre im Schulunterricht umsetzen? Erstellen Sie einen Unterrichtsentwurf für die Sekundarstufe I.

Der Unterricht teilt sich ein in 3 Einheiten:
Einleitung (5 min),
Hauptteil (25 min)
und Schluss (15 min).

In der Einleitung wird die Problemstellung (Verschlüsselung der Nachricht von Caesar) thematisiert und zusammen mit der Klasse werden die Verschlüsselungstechniken durch das Sammeln von Ideen erarbeitet.
Im Hauptteil bearbeiten die Schüler und Schülerinnen einen Text, den sie selbst entschlüsseln müssen. Dieser beinhaltet 3 Verschlüsselungstechniken: Ceasar-, Skytala-Verschlüsselung und Gartenzaun-Chiffre. Dabei variieren die Bedingungen während der Bearbeitung. Die Caeser-Verschlüsselung kann durch eine Drehplatte mit zwei Buchstabenreihen veranschaulicht werden. Bei der Skytala-Verschlüsselung können die Radien der Rohre verändert werden, um die Komplexität des Entschlüsselns hervorzuheben. Die Gartenzaun-Chiffre lässt sich durch die Höhe des "Zauns" verändern.
Im Schluss geht es um die Anwendung der Entschlüsselungsmethode, indem die Schüler und Schülerinnen einen Textentwurf an den Sitznachbar anfertigen. Anschließend folgt eine Diskussion über den Zweck und Nutzen einer Verschlüsselung.

Polyalphabetische Verschlüsselung

Verschlüsseln mit Zufallsexperimenten

Beispiel:
Gegeben sei das Klartextalphabet $A:=\{A,N,S\}$ und der Klartext $\omega =(A,N,A,N,A,S)\in A^{+}$.
Das Häufigkeitsprofil dieses Textes sieht folgendermaßen aus:

Buchstabe	Häufigkeit
A	$\frac{3}{6}=\frac{1}{2}$
N	$\frac{2}{6}=\frac{1}{3}$
S	$\frac{1}{6}$

Ziel: Jeder Buchstabe im Geheimtext soll mit der gleichen Häufigkeit vorkommen, sodass eine Kryptoanalyse über das Sprachprofil nicht möglich ist.

Sei nun das Geheimtextalphabet $B:=\{1,2,3,...,12\}$ und der Schlüssel zur Verschlüsselung des Klartextes sei folgendermaßen definiert:

Klartextbuchstabe	Menge der zugeordneten Geheimtextbuchstaben	Anzahl der zugeordneten Geheimalphabetbuchstaben	Anteil
A	$\{1,3,8,9,11,12\}={\mathrm{\Omega }}_A$	$6=|{\mathrm{\Omega }}_A|$	$\frac{|{\mathrm{\Omega }}_A|}{|B|}=\frac{6}{12}=\frac{1}{2}$
N	$\{2,5,7,10\}={\mathrm{\Omega }}_N$	$4=|{\mathrm{\Omega }}_N|$	$\frac{|{\mathrm{\Omega }}_N|}{|B|}=\frac{4}{12}=\frac{1}{3}$
S	$\{4,6\}={\mathrm{\Omega }}_S$	$2=|{\mathrm{\Omega }}_S|$	$\frac{|{\mathrm{\Omega }}_S|}{|B|}=\frac{2}{12}=\frac{1}{6}$

Um den Klartext zu verschlüsseln, werden Zufallsexperimente verwendet, um jeweils einen der jeweils zugeordneten Geheimtextbuchtaben zufällig auszuwählen.
Zur Verschlüsselung des Buchtabens "A" benötigen wir ein Zufallsexperiment, bei dem jedes Ereignis mit der Wahrscheinlichkeit $\frac{1}{6}$ eintritt, sodass jeder der 6 Geheimtextbuchstaben mit der gleichen Wahrscheinlichkeit ausgewählt werden könnte. Als Zufallsgenerator könnte ein Würfel gewählt werden und zeigt der Würfel beispielsweise die Augenzahl 1, wird beispielsweise der Geheimtextbuchstabe "1" zugeordnet, bei einer 2 wird der Geheimtextbuchstabe "3" zugeordnet usw.
Zur Verschlüsselung des Buchtabens "N" benötigen wir ein Zufallsexperiment, bei dem jedes Ereignis mit der Wahrscheinlichkeit $\frac{1}{4}$ eintritt, sodass jeder der 4 Geheimtextbuchstaben mit der gleichen Wahrscheinlichkeit ausgewählt werden könnte. Als Zufallsgenerator könnte blind aus einer Urne mit 4 Kugeln gezogen werden, die mir den Ziffern "2", "5", "7" und "10" beschriftet sind.
Zur Verschlüsselung des Buchtabens "S" benötigen wir ein Zufallsexperiment, bei dem jedes Ereignis mit der Wahrscheinlichkeit $\frac{1}{2}$ eintritt, sodass jeder der 2 Geheimtextbuchstaben mit der gleichen Wahrscheinlichkeit ausgewählt werden könnte. Als Zufallsgenerator könnte eine faire Münze gewählt werden, bei Kopf könnte der Geheimtextbuchstabe "4", bei Zahl der Geheimtextbuchstabe "6" gewählt werden.
Wird auf diese Weise verschlüsselt, kommt jeder Buchstabe aus B im Geheimtext mit einer Häufigkeit von etwa $\frac{1}{12}$ vor.

Definition: σ-Algebra
Sei $\mathrm{\Omega }$ eine nichtleere Menge und sei $𝒫(\mathrm{\Omega })$ die Potenzmenge dieser Menge.

Ein Mengensystem $𝒮\subset 𝒫(\mathrm{\Omega })$, also eine Menge von Teilmengen von $\mathrm{\Omega }$, heißt σ-Algebra (auf oder über $\mathrm{\Omega }$), wenn es die folgenden drei Bedingungen erfüllt:

• (1) $𝒮$ enthält die Grundmenge. Es gilt also $\mathrm{\Omega }\in 𝒮$
• (2) $𝒮$ ist stabil bezüglich der Komplementbildung. Ist also $S\in 𝒮$, so ist auch $S^{𝖼}=\mathrm{\Omega }\setminus S$ in $𝒮$ enthalten.
• (3) $𝒮$ ist stabil bezüglich abzählbarenVereinigungen. Sind also Mengen

$S_1,S_2,S_3,\dots$ in $𝒮$ enthalten, so ist auch $\bigcup _{i=1}^{\mathrm{\infty }}{S}_i$ in $𝒮$ enthalten.

Ziel: Man möchte nicht nur einzelnen Buchstaben $\omega \in \mathrm{\Omega }$ eine Wahrscheinlichkeit zuordnen, sondern auch Teilmengen des Alphabets.

Beispiele: Bei folgenden Mengen handelt es sich um σ-Algebren:

• $\{\mathrm{\varnothing },\mathrm{\Omega }\}$
• $\{\mathrm{\varnothing },A,A^C,\mathrm{\Omega }\}$
• $\{\mathrm{\varnothing },ℝ,[0,1],(-\mathrm{\infty },0)\cup (1,\mathrm{\infty })\}$

Definition: Wahrscheinlichkeitsraum $(\mathrm{\Omega },𝒮,P)$
Sei $\mathrm{\Omega }$ (ein Alphabet) eine nichtleere Menge und $𝒮$ eine σ-Algebra über $\mathrm{\Omega }$.
Ferner gibt es eine Abbildung $P$ mit

• (1) $P:𝒮\to [0,1]$

$E\mapsto P(E)$.

$P$ ordnet jeder Menge $E\in 𝒮$ einen Wahrscheinlichkeitswert zu.

• (2) $P(\mathrm{\Omega })=1$. Die Wahrscheinlichkeit, dass ein Buchstabe aus dem Alphabet $\mathrm{\Omega }$ stammt, ist 1.
• (3) $\mathrm{\forall }{E}_n\in 𝒮,n\in \mathbb{N}:E_n$ paarweise disjunkt $\Rightarrow P(\bigcup _{n\in \mathbb{N}}{E}_n)=\sum _{n\in \mathbb{N}}P(E_n)$
  

Beispiel: Münzwurf (einfaches Werfen mit einer fairen Münze).
$\mathrm{\Omega }=\{K,Z\},𝒮=\{\mathrm{\varnothing },\{K\},\{Z\},\{K,Z\}\}$
Es gilt:

• (1) $P:𝒮\to [0,1]$

$\mathrm{\varnothing }\mapsto 0$

$\{K\}\mapsto \frac{1}{2}$

$\{Z\}\mapsto \frac{1}{2}$

$\{K,Z\}\mapsto 1$

• (2) $P(\{K,Z\})=1$
• (3) Es gilt: $\{K\}$ und $\{Z\}$ p.w.d. $\Rightarrow P(\{K\}\cup \{Z\})=P(\{K,Z\})=1=\frac{1}{2}+\frac{1}{2}=P(\{K\})+P(\{Z\})$

Definition: Trägermenge, Wahrscheinlichkeitsverteilung
Sei $(\mathrm{\Omega },𝒮,P)$ ein diskreter Wahrscheinlichkeitsraum, dann definiert man den Träger $Tr(P)$ wie folgt: $Tr(P):=\{\omega \in \mathrm{\Omega }\mid P(\{\omega \})>0\}$.

Beispiel: Münzwurf (einfaches Werfen mit einer fairen Münze).
Sei $\mathrm{\Omega }=\{K,Z,R\}$ mit $P(R)=0$, R: Rand der Münze. Dann ist $Tr(P)=\{K,Z\}$.

Satz: Träger und Geheimtexte
Sei $A$ das Klartextalphabet und $B$ das Geheimtextalphabet. Ferner sei ein stochastischer Schlüssel
$f:A{\to }_{P}B$

$x{\mapsto }_P({\mathrm{\Omega }}_x,{𝒮}_x,P_x)$

gegeben, dann sind alle Geheimtexte aus der Menge ${\mathrm{\Omega }}^{+}$ mit $\mathrm{\Omega }=\bigcup _{x\in A}Tr(P_x)$.

Beweis: Träger und Geheimtexte
Dem Satz entnehmen wir, $A$ ist das Klartextalphabet und $B$ das Geheimtextalphabet.
Es gilt:

• (1) $\mathrm{\forall }x\in A:y\in B\wedge f(x)=y\wedge P_x(\{y\})>0$ für die Abbildung $P_x$
  
• (2) Für den Klartext gilt:
  

$\omega =({\omega }_1,{\omega }_2,...,{\omega }_n)\in A^{+}$

• (3) Für den Chiffretext gilt:
  

$(f({\omega }_1),f({\omega }_2),...,f({\omega }_n))\in B^{+}$ mit $y_1=f({\omega }_1),y_2=f({\omega }_2),...,y_n=f({\omega }_n)$

• (4) Für die Trägermenge gilt:
  

$y_1\in Tr(P_{{\omega }_1})\wedge y_2\in Tr(P_{{\omega }_2}),...,\wedge y_{\omega }\in Tr(P_{{\omega }_n})$

• (5) Daraus Folgt:
  

$\Rightarrow \mathrm{\forall }k\in \{1,2,3,...,n\}:y_k\in Tr(P_{{\omega }_k})$

$\Rightarrow \mathrm{\forall }k\in \{1,2,3,...,n\}:y_k\in \bigcup _{i=1}^{n}Tr(P_{{\omega }_i})$

$\Rightarrow \mathrm{\forall }k\in \{1,2,3,...,n\}:y_k\in \mathrm{\Omega }$

$\Rightarrow y=(y_1,y_2,y_3,...,y_n)\in {\mathrm{\Omega }}^{+}$

q.e.d.

Satz: Eindeutigkeit der Entschlüsselung mit stochastischen Schlüsseln
Sei $A$ das Klartextalphabet und $B$ das Geheimtextalphabet und
$f:A{\to }_{P}B$

$x{\mapsto }_P({\mathrm{\Omega }}_x,{𝒮}_x,P_x).$

• (1) Die Dechiffrierung ist genau dann eindeutig, wenn die Trägermenge $Tr(P_x)$ für alle $x\in A$ paarweise disjunkt sind.
• (2) Gilt die Bedingung (1), existiert eine Abbildung

$f^{-1}:\mathrm{\Omega }\to A$

$x\mapsto f^{-1}(x)$

mit $\mathrm{\Omega }:=\bigcup _{x\in A}Tr(P_x)$ für die Entschlüsselung von Geheimtexten $y=(y_1,...,y_n)\in B^{+}$, die mit $f$ verschlüsselt werden.

Bew: Eindeutigkeit der Entschlüsselung mit stochastischen Schlüsseln
(1) Die erste Aussage ist eine genau dann Aussauge. Zunächst beweisen wir die Rückrichtung und danach die Hinrichtung.

"$\Leftarrow$" Seien für alle $x\in A$ die Trägermengen $Tr(P_x)$ paarweise disjunkt.

Aus dem Satz für Träger und Geheimtexte folgt

$\mathrm{\forall }y=(y_1,...,y_n)\in B^{+}:y\in {\mathrm{\Omega }}^{+}$ mit ${\mathrm{\Omega }}^{+}=\bigcup _{x\in A}Tr(P_x)$

$\Rightarrow \mathrm{\forall }{y}_k,k\in \{1,...,n\}\mathrm{\exists }!Tr(P_{x_k}):y_k\in Tr(P_{x_k})$

$\Rightarrow \mathrm{\forall }{y}_k\in \{1,...,n\}:y_k\in {\mathrm{\Omega }}_{x_k}$

$\Rightarrow$ Das Klartextzeichen zu $y_k$ ist $x_k$

Durch den stochastischen Schlüssel entsteht für jedes Klartextzeichen $x_k$ der Wahrscheinlichkeitsraum $({\mathrm{\Omega }}_{x_k},S_{x_k},P_{x_k})$.

"$\Rightarrow$" Sei die Entschlüsselung eindeutig.

Wir nehmen nun an, dass die Trägermengen $Tr(P_x)$ nicht paarweise disjunkt sind und zeigen, dass dies zum Widerspruch führt.

$\Rightarrow \mathrm{\exists }y\in B,\mathrm{\exists }{x}_1,x_2\in A:y\in Tr(P_{x_1})\cap Tr(P_{x_2})\ne \mathrm{\varnothing }$

$\Rightarrow y\in Tr(P_{x_1})\wedge y\in Tr(P_{x_2})$

Damit ist das $y$ durch Verschlüsselung mit $({\mathrm{\Omega }}_{x_1},S_{x_1},P_{x_1})$ und $({\mathrm{\Omega }}_{x_2},S_{x_2},P_{x_2})$ entstanden.

Es ist also nicht möglich dem $y$ eindeutig ein $x\in B$ zuzuordnen.

(2) Für die zweite Aussage zeigen wir nun, dass so eine Abbildung $f^{-1}$ (die jedem verschlüsselten $y\in B$ wieder ein eindeutiges Klartextzeichen
$x\in A$ zuordnet) existiert, falls Bedingung (1) erfüllt ist.

Seien für alle $x\in A$ die Trägermengen $Tr(P_x)$ paarweise disjunkt und $\mathrm{\Omega }:=\bigcup \mathrm{\backslash limits}x\in ATr(P_x)$.

$\Rightarrow \mathrm{\forall }y\in \mathrm{\Omega }\mathrm{\exists }!x\in A:y\in Tr(P_x)$

Definiere also

$f^{-1}:\mathrm{\Omega }\to A,y\to x,$falls$y\in Tr(P_x)$

$◻$

Verschlüsselung beliebiger digitaler Daten

[Verwendung von GNU Octave.]

Definition: p-adisches Stellenwertsystem

Sei $z\in {\mathbb{N}}_0$ gegeben.
$z$ besitzt in dem $p$-adischen Stellenwertsystem die Darstellung $(z_n,z_{n-1},...,z_1,z_0{)}_p$, wenn gilt: $z_n,z_{n-1},...,z_1,z_0\in \{0,1,...,p-1\}$.
$z=\sum _{k=0}^{\mathrm{\infty }}{z}_k\cdot p^k$ mit $z_k\in \{0,1,...,p-1\}$.

Beispiel: Umrechnung von $43210_5$ in das Dezimalsystem

Jede Stelle hat den Wert der entsprechenden Fünferpotenz. Die der ersten Ziffer von rechts entsprechende Potenz ist $5^0=1$.
Vorgehen: Multipliziere jede Ziffer mit der entsprechenden Potenz und summiere. Gehe am besten von rechts nach links vor:

$0\cdot 5^0+1\cdot 5^1+2\cdot 5^2+3\cdot 5^3+4\cdot 5^4$

$=0\cdot 1+1\cdot 5+2\cdot 25+3\cdot 125+4\cdot 625$
$=0+5+50+375+2500$
$=2930$
Ergebnis: $43210_5=2930_{10}$

Beispiel: Umrechnung von $375_{10}$ in das Binärsystem

Vorgehen: (1) Teile die Zahl mit Rest durch die Basis 2. (2) Der Divistionsrest ist die Ziffer im Binärsystem (von rechts nach links). (3) Falls der (ganzzahlige) Quotient 0 ist, ist das Verfahren beendet, ansonsten nimm den (ganzzahligen) Quotienten als neue Zahl und wiederhole ab (1).
$375:2=187Rest1$
$187:2=93Rest1$
$93:2=46Rest1$
$46:2=23Rest0$
$23:2=11Rest1$
$11:2=5Rest1$
$5:2=2Rest1$
$2:2=1Rest0$
$1:2=0Rest1$
Ergebnis: $375_{10}=101110111_2$

Nebenbei:
- There are only 10 types of people in the world: those who understand binary, and those who don't. -
- Why do mathematicians confuse Halloween and Christmas? - Because 31 Oct = 25 Dec. -

Definition: Kodierung reeller Zahlen im p-adischen Stellenwertsystem

Sei $z\in {ℝ}^{+}$ gegeben.
$(z_n,z_{n-1},...,z_1,z_0,z_{-1},z_{-2},...{)}_p$ stellt die Zahl $z$ wie folgt dar:
$z=\sum _{k=-\mathrm{\infty }}^n{z}_k\cdot p^k$ mit $z_k\in \{0,1,...,p-1\}$.

Verschlüsseln von digitalen Bytefolgen

Bilder

Graustufen werden durch Werte zwischen 0 und 255 kodiert. Farben können analog durch 24 bit dargestellt werden.

Beispiel zur Verschlüsselung digitaler Daten: Bildverschlüsselung

Texte

Die Zuordnung von Buchstaben und Sonderzeichen (Alphabet $B$) nach $\tilde{A}$ erfolgt über eine bijektive Abbildung (Schlüssel):
$f:B\to \tilde{A}$

$z\mapsto f(z)$

Bei diesem bijektiven Schlüssel geht es nicht um Geheimhaltung, sondern um Standardisierung.
Beispiel: ASCII-Code.

Audio

Definition: Digitalisierung eines Audiosignals

Sei $f:[a,b]\to [c,d]$ ein analoges Audiosignal und $(x_1,...,x_n)$ eine äquidistante Unterteilung von $[a,b]$ mit $x_1=a$ und $x_n=b$.
$(f(x_1),...,f(x_n))\in [c,d{]}^n$
Ferner sei $(y_1,...,y_n)$ eine äquidistante Unterteilung von $[c,d]$ mit $f(x_1),...,f(x_n)\in \{y_1,...,y_n\}$.

Videos

Video entsteht aus einer Folge von Einzelbildern und einem Audiosignal.

Integrität von Daten

Ziel: Nachricht von Sender A an B zu übermitteln und B möchte sicher sein, dass die Daten nicht verändert wurden.

Überprüfung über die Quersumme - Übermittlung mit digitaler Unterschrift

Definition: Gewichtete Quersumme

Sei $a=(a_1,...,a_n)\in {\mathbb{N}}_0^n$ ein Tupel aus natürlichen Zahlen. $r=(r_1,...,r_n)\in {ℝ}^n$.
$\sum _{k=1}^n{a}_k\cdot r_k=a\cdot r^T=(a_1,...,a_n)\cdot \left(\begin{array}{c}{r}_1\\ ⋮\\ r_n\end{array}\right)$ nennt man gewichtete Quersumme mit $r\in {ℝ}^n$.

Ziel: Durch die gewichtete Quersumme kann man die Restklasse bei der Division durch n bestimmen. Die Restklasse ist eine digitale Unterschrift der p-adischen Zahlenfolge.

Definition: Gewichtete Quersumme für Restklassen

Sei $(z_n,...,z_0)\in (0,...,p-1{)}^{n+1}$ sei eine Ziffernfolge im p-adischen System. $r_n:=p^{n}modm$ mit $r_n\in \{0,...,m-1\}$.
$\tilde{r}=\sum _{k=0}^n{r}_k\cdot z_{k}modm$ mit $\tilde{r}\in \{0,...,n-1\}$.
$\sum _{k=0}^n{r}_k\cdot z_k$ ist die gewichtete Quersumme bei Division durch $m$.
$\tilde{r}$ ist die digitale Unterschrift für $(z_n,...,z_0)$ mit Schlüssel $m\in \mathbb{N},m>1$.
Die Gewichte der Quersumme sind periodisch.

Satz: Perioden in Quersummenregeln

Sei $r:=(r_k{)}_{k\in \mathbb{N}}\in \{0,...,m-1{\}}^{{\mathbb{N}}_0}$.
$r_k\equiv p^{k}modm$ (Rest, den die Bündelungseinheit $p^k$ bei Division durch $m$ lässt.)
Dann gibt es ab einer bestimmten Indexschranke eine Periode in der Folge der $r_k$.

Beweis: Perioden in Quersummenregeln
Seien $r_0,r_1,...,r_{m-1}$ die ersten m Reste aus $(r_k{)}_{k\in {\mathbb{N}}_0}$.
Bei der Division durch m muss mindestens bei m+1 ein Rest doppelt auftreten, da die Anzahl der Reste endlich ist. Reste $(0,1,...,m-1)$.
Ohne Einschränkung gelte: $r_m=r_i$. mit $i\in \{0,...,m-1\}$.
(Wir gehen einfach davon aus, dass dieser Rest doppelt vorkommt.)

$r_0,r_1,...,r_i,r_{i+1},...,r_{m-1},r_m,r_{m+1},...$.
$r_{i+1}\equiv p^{i+1}\equiv p^i\cdot p^i\equiv r_i\cdot p^1\equiv r_m\cdot p^1\equiv p^m\cdot p^1\equiv p^{m+1}\equiv r_{m+1}modm$.

Man erhält mit $r_{i+1}=r_{m+1}$ auch $r_{i+2}=r_{m+2}$.

$r_{i+2}\equiv p^{i+2}\equiv p^{i+1}\cdot p^1\equiv r_{i+1}\cdot p^1\equiv r_{m+1}\cdot p^1\equiv p^{m+1}\cdot p^1\equiv p^{m+2}\equiv r_{m+2}modm$.

Man erhält sukzessiv:
$r_0,r_1,...,r_i,r_{i+1},...,r_{m-1},r_m,r_{m+1},...,r_{2m-1},r_{2m},...$.
$r_{i+k}\equiv r_{m+k}$ für alle $k\in {\mathbb{N}}_0$.

Damit haben wir eine Periode der Länge $l\le m-i$.
q.e.d.

Asymmetrische Verschlüsselung

Definition: Public-Key-Kryptosystem oder Asymmetrisches Kryptosystem

In einem Public-Key-Kryptosystem hat jeder Teilnehmer $T$ ein Paar von Schlüsseln:

• einen öffentlichen Schlüssel $E:=E_T$ zur Verschlüsselung und
• einen privaten Schlüssel $D:=D_T$ zum Entschlüsseln,

die sich durch folgende entscheidende Public-Key-Eigenschaft auszeichnen:
Aus der Kenntnis des öffentlichen Schlüssels $E_T$ ist der private Schlüssel $D_T$ nicht zu erschließen.

Definition: Public-Key-Verschlüsselungssystem

Ein asymmetrisches Kryptosystem heißt Public-Key-Verschlüsselungssystem (asymmetrisches Verschlüsselungssystem), falls für jede Nachricht $m$ gilt:
Wenn $c=E(m)$ ist, dann gilt $D(c)=m$, d.h. $D(E(m))=c$.
Die mit $E$ verschlüsselte Nachricht wird mittels $D$ wieder korrekt entschlüsselt.

Der RSA-Algorithmus

Das Verfahren

Beispiel:

(1) Schlüsselerzeugung

(a)   p = 11 ; q = 13

(b)   N = p · q = 11 · 13 = 143

(c)   $\phi$(N) = (p-1) · (q-1) = 10 · 12 = 120

(d)   e = 23

Euklidischer Algorithmus:

120 = 5 · 23 + 5
 23 = 5 · 5 + 3
  5 = 1 · 3 + 2
  3 = 1 · 2 + 1
  2 = 2 · 1 + 0    → Abbruchbedingung
   ggT (120;23)

 e · d = 1 mod $\phi$(N)

Ziel: 1 = d · 23 + y · 120

(e)     1 = 3 - 1 · 2 = (23- 4 · 5) - (5 - 1 · 3)
          = 23 - 4 · 5 + 1 · 3 = 23 - 5 · (120 - 5 · 23) + (23 - 4 · 5)
          = 23 - 5 · 120 + 25 · 23 + 23 - 4 · (120 - 5 · 23)
          = 47 · 23 - 9 · 120

(f)    (e; N) = (23,143); (d,N) = (47,143)

(2) Verschlüsseln der Klartextnachricht K = 7

        c $\equiv$   Ke mod N  $\equiv$  723 mod 143
                        $\equiv$  721 · 72 mod 143
                        $\equiv$  (77)3 · 72 mode 143
                        $\equiv$  63 · 72 mod 143
                        $\equiv$  73 · 49 mod 143
                        $\equiv$  2 mod 143

(3) Entschlüsseln der Geheimbotschaft c = 2

           K $\equiv$  cd mod N $\equiv$  247 mod 143
                         $\equiv$  2(6 · 7) · 25 mod 143
                         $\equiv$  7 mod 143

Die Mathematik hinter dem RSA-Algorithmus

Definition: Eulersche $\phi$-Funktion

$\phi (n):=|G_n|$ mit $G_n:=\{k\in \mathbb{N}\mid ggT(n,k)=1,k\le n\}$.
$\phi (n)$ gibt die Menge aller Zahlen $k\in \mathbb{N}$ mit $k\le n$ an, die teilerfremd zu $n$ sind.

Satz: $\phi$-Funktion und Primzahlen
b Sei $p\in \mathbb{N}$ eine Primzahl ($p\in \mathbb{P}$), dann gilt: $\phi (p)=p-1$.

Beweis: $\phi$-Funktion und Primzahlen
z.Z. $\phi (p)$=|$G_p|=p-1$
In $G_p$ können $1,...,p-1,p$, also $p$ mögliche Zahlen liegen.
$G_p$:={$k\in \mathbb{N}$$|ggT(p,k)=1$, $k\le p$}
Es gilt: $p\notin G_p$, da $ggT(p,p)=p$ (für $p>1$) gilt.
$1\in G_p$, da für alle $p\in \mathbb{N}$ gilt: $ggT(p,1)=1$
Für alle $k\in \{2,...,p-1\}$ gilt ebenfalls $ggT(p,k)=1$, denn sonst wäre $p$ keine Primzahl und hätte den Teiler $k$ mit $k|p\wedge 1<k<p.$
Also gilt:$\phi (p)=p-1.$

Satz: Multiplikativitätssatz der $\phi$-Funktion

Seien $p,q\in \mathbb{P}$ gegeben, dann gilt $\phi (p\cdot q)=\phi (p)\cdot \phi (q)$.

Beweis: z.Z.: Seien $p,q\in \mathbb{P}$ Primzahlen: $\phi (p\cdot q)=\phi (p)\cdot \phi (q)$.

In $G_{pq}$ können nur die Elemente $1,...,pq-1,pq$ also $pq$ Elemente enthalten sein $(|G_{pq}|\le pq)$.

Nun schließen wir aus dieser Menge Elemente aus, die nicht in $G_{pq}$ enthalten sein können:

Es gilt $pq\notin G_{pq}$, da $ggT(pq,pq)=pg\ne 1$.

Es bleiben als mögliche Zahlen $G_{pq}\subseteq 1,...,pq-1:=M_{pq};|M_{pq}|=pq-1$

Wir betrachten alle Zahlen, die nicht Teilerfremd zu pq sind.

$1\cdot p,2\cdot p,...,(q-1)p$ also $q-1$ nicht Teilerfremde Zahlen aus $M_{pq}$

$1\cdot q,2\cdot q,...,(p-1)q$ also $p-1$ nicht Teilerfremde Zahlen aus $M_{pq}$

Dabei kommt keine Zahl doppelt vor.

Damit folgt für die Anzahl der Elemente in $|G_{pq}|=|M_{pq}|-(q-1)-(p-1)$.

Durch Umformung ergibt sich nun: $|G_{pq}|=|M_{pq}|-(q-1)-(p-1)=pq-1-q+1-p+1=pq-q-p+1=q(p-1)-p+1=q(p-1)-1(p-1)=(p-1)(q-1)$

Definition: Gruppe

Eine Gruppe ist ein Paar $(G,*)$ bestehend aus einer Menge $G$ und einer (inneren) Verknüpfung $*$ auf $G$.
Das heißt, durch $*$ wird die Abbildung $*:G\times G\to G,(a,b)\mapsto a*b$ beschrieben.
Erfüllt die Verknüpfung die folgenden Axiome, dann wird $(G,*)$ Gruppe genannt:

• (AG) Für alle Gruppenelemente $a$, $b$ und $c$ gilt: $(a*b)*c=a*(b*c).$
• (NE) Es gibt ein neutrales Element $e\in G$, mit dem für alle Gruppenelemente $a\in G$ gilt: $a*e=e*a=a$.
• (IE) Zu jedem Gruppenelement $a\in G$ existiert ein inverses Element $a^{-1}\in G$ mit $a*a^{-1}=a^{-1}*a=e$.

Definition: Abelsche Gruppe

Eine Gruppe $(G,*)$ heißt abelsch oder kommutativ, wenn zusätzlich das folgende Axiom erfüllt ist:

• (KG) Für alle Gruppenelemente $a$ und $b$ gilt $a*b=b*a$.
  

Definition: Potenzen in Gruppen

Sei $(G,*)$ eine Gruppe. Dann definiert man:
$a^n:=\underset{n-fach}{\underbrace{a*a*...*a}}=((...((a*a)*a)*...*a)$ für $n\in \mathbb{N}$.
$a^{-n}:=\underset{n-fach}{\underbrace{a^{-1}*a^{-1}*...*a^{-1}}}=((...((a^{-1}*a^{-1})*a^{-1})*...*a^{-1})$ für $n\in \mathbb{N}$.
$a^0:=e$

Definition: Untergruppe
Sei $(G,*)$ eine Gruppe.
$\mathrm{\varnothing }\ne U\subseteq G$ heißt Untergruppe $(U,*)$ von $(G,*)$ $:\iff \mathrm{\forall }a,b\in U:a*b^{-1}\in U$.

oder

Sei $(G,*)$ eine Gruppe und $U$ eine nicht leere Teilmenge von $G$.
$(U,*)$ heißt Untergruppe von $(G,*)$ $:\iff$

• (IV) Durch $*$ wird die Abbildung $*:U\times U\to U,(a,b)\mapsto a*b$ beschrieben.
• (AG) Für alle Gruppenelemente $a$, $b$ und $c$ gilt: $(a*b)*c=a*(b*c).$
• (NE) Es gibt ein neutrales Element $e\in U$, mit dem für alle Gruppenelemente $a\in U$ gilt: $a*e=e*a=a$.
• (IE) Zu jedem Gruppenelement $a\in U$ existiert ein inverses Element $a^{-1}\in U$ mit $a*a^{-1}=a^{-1}*a=e$.
  

Satz: Neutrales Element der Untergruppe
Wenn $(U,*)$ Untergruppe der Gruppe $(G,*)$ ist, dann besitzt $(U,*)$ das gleiche neutrale Element $e$ wie $(G,*)$.

Definition: Faktorgruppe
Sei $(G,*)$ eine Gruppe und $(U,*)$ eine Untergruppe von $(G,*)$, dann nennt man $G/U$ Faktorgruppe (mit $(G,*)$ kommutativ). Die Faktorgruppe enthält folgende Elemente:
$G/U:=\{a*U\mid a\in G\}$.
$a*U$ nennt man Nebenklasse von $U$.

Satz von Euler bzw. kleiner Satz von Fermat
Seien $m,n\in \mathbb{N}$ gegeben mit $ggT(m,n)=1$.
Dann gilt: $m^{\phi (n)}\equiv 1modn$

Satz Gruppe bezüglich $\phi (n)$
Sei $n\in \mathbb{N},n\ge 1$ gegeben.
$(R_n,\cdot )$ sei das multiplikative Verknüpfungsgebilde der Restklassen
$R_n=\{{\overline{0}}_n,{\overline{1}}_n,...,{\overline{n-1}}_n\}$, dann gilt:
$R_n^{*}=\{{\overline{z}}_n\mid z\in T_n=\{z\in \mathbb{N}\mid (z\le n)\wedge ggT(z,n)=1\}\}$
ist eine abelsche Gruppe mit $\phi (n)$ Elementen.
Die abelsche Gruppe $(R_n,\cdot )$ nennt man reduziertes Restsystem.

Beweis:
z.z.: $(R_n^{*},\cdot )$ ist eine abelsche Gruppe.

• (IV) z.z.: Durch $\cdot$ wird die Abbildung $\cdot :R_n^{*}\times R_n^{*}\to R_n^{*},(a,b)\mapsto a\cdot b$ beschrieben mit $a:={\overline{a}}_n$ und $b:={\overline{b}}_n$.

Es muss also gezeigt werden: $a\cdot b={\overline{a}}_n\cdot {\overline{b}}_n=(\overline{a\cdot b}{)}_n\in R_n^{*}$.

Vorüberlegungen:

• Ohne Einschränkung können wir später für $a\cdot b$ einen Repräsentanten aus $\{0,...,n-1\}$ wählen.
  
• Zu zeigen ist: $ggT(a,n)=1\wedge ggT(b,n)=1\Rightarrow ggT(a\cdot b,n)=1$, bzw. dass für $a\cdot b=k\cdot n+r$ gilt: $ggT(r,n)=1$, denn dann gilt ${\overline{r}}_n\in R_n^{*}$.
  
• $M_T(a)=\{t\in \mathbb{N}\mid t|a\}$ (Teilermenge von $a$). $M_T(b)\cap M_T(n)=\{1\}=M_T(a)\cap M_T(n)$.
• $a\cdot b$ kann auch keine gemeinsamen Teiler mit $n$ besitzen, da $M_T(a),M_T(b)\subseteq M_T(a\cdot b)$
  

• (AG) z.z.: Für alle Gruppenelemente $a,b,c\in R_n^{*}$ gilt: $(a\cdot b)\cdot c=a\cdot (b\cdot c).$

Das Assoziativgesetz ist in $(R_n^{*},\cdot )$ erfüllt, weil es in der Gruppe $(R_n,\cdot )$ gilt.

• (KG) z.z.: Für alle Gruppenelemente $a,b\in R_n^{*}$ gilt: $a\cdot b=b\cdot a.$

Das Kommutativgestetz ist in $(R_n^{*},\cdot )$ erfüllt, weil es in der abelschen Gruppe $(R_n,\cdot )$ gilt.

• (NE) z.z.: Es gibt ein neutrales Element $e\in R_n^{*}$, mit dem für alle Gruppenelemente $a\in R_n^{*}$ gilt: $a\cdot e=e\cdot a=a$.

Sei $e={\overline{1}}_n$. Es gilt: $a\cdot e={\overline{a}}_n\cdot {\overline{1}}_n={\overline{1}}_n\cdot {\overline{a}}_n={\overline{a}}_n=a$ und ${\overline{1}}_n\in R_n^{*}$, da $ggT(1,n)=1$.

• (IE) z.z.: Zu jedem Gruppenelement $a\in R_n^{*}$ existiert ein inverses Element $a^{-1}\in R_n^{*}$ mit $a\cdot a^{-1}=a^{-1}\cdot a=e$.

Da $ggT(a,n)=1$ für ${\overline{a}}_n\in R_n^{*}$, kann man ein modulares Inverses $a^{-1}$ bestimmen mit $ggT(a^{-1},n)=1$, also $a^{-1}\in R_n^{*}$, und $a\cdot a^{-1}={\overline{a}}_n\cdot {\overline{a^{-1}}}_n={\overline{a^{-1}}}_n\cdot {\overline{a}}_n=a^{-1}\cdot a=e={\overline{1}}_n$.

Insgesamt ist $(R_n^{*},\cdot )$ ist eine abelsche (multiplikative) Gruppe.

Bemerkung: $R_n^{*}$ hängt mit $T_n$ wie folgt zusammen: $T_n$ ist ein Repräsentantensystem für $R_n^{*}$.

Definition: Repräsentantensystem
Sei $z,n>1$ mit $n\in \mathbb{N}$ gegeben.
Wir betrachten die Restklassen $R_{n}modn$.
Sei $T^{*}\subseteq R_n$ und $T\subseteq \mathbb{Z}$.
$T$ heißt Repräsentantensystem von $T^{*}:\iff (\{{\overline{z}}_n\mid z\in T\}=T^{*})\wedge (\mathrm{\forall }z,y\in T:z\ne y\to {\overline{z}}_n\ne {\overline{y}}_n)$.
Damit gilt insgesamt $\phi (n)=|R_n^{*}|,R^{*}$ Gruppe.

Satz: Nachrichtenmenge
Mit dem RSA-Algorithmus können Mengen $\{0,1,...,k\}$ mit $k=\min \{p,q\}-1$ und $n=p\cdot q$ verschlüsselt werden.

Beweis: Nachrichtenmenge
Nach der Methode der Schlüsselgenerierung wird $n=p\cdot q$ mit $p,q\in P$ als Produkt von zwei Primzahlen $p$ und $q$ erzeugt, wobei $p\ne q$.
$T(n)=T(p,q)=\{1,p,q,p\cdot q\}$ ist die Teilmenge von $n$.
$ggT(p,K)=1$

1.Fall: $p<q$ Alle Zahlen $\{1,...,p-1\}$ sind Teilerfremd zu $p,q$ und $n$.
2.Fall: $p>q$ Alle Zahlen $\{1,...,q-1\}$ sind Teilbar zu $p,q$ und $n$.
3.Fall: $p=q$ Muss nicht geprüft werden, da $p\ne q$ gilt. Trifft trotzdem zu.
Wenn $p=q$, dann gilt: $T(n)=T(p\cdot q)=T(p^2)=\{1,p,p^2\}$. Alle Zahlen $\{1,...,p-1\}$ sind Teilerfremd zu $p,q$ und $n$.
$K=min\{p,q\}-1$, um $p$ und $q$ auszuschließen.
Dann gilt: $ggT(p,n)=p\ne 1$ und $ggT(q,n)=q\ne 1$.

Definition: Ordnung eines Elements
Sei $U=<a>$ und $a\in G$ mit $(G,*)$ Gruppe.
$Ord(a)=|U|=k$ mit $k:=\min \{\tilde{k}\in \mathbb{N}\mid a^{\tilde{k}}=e\}.$

Satz: Lagrange
Sei $(G,*)$ eine abelsche Gruppe und $U$ eine Untergruppe von $G$, dann gilt:
$|U|\mid |G|$

Beweis:

Idee: Disjunkte Zerlegung von $G$ in gleichmächtige Mengen.

• Zerlegung von $G$ in Teilmengen durch die Zerlegung in Nebenklassen

Wir betrachten die Nebenklassen $a*U$ mit $a\in G$ und $U$ Untergruppe von $G$.

z.z.: $\bigcup _{a\in G}a*U=G$

Beweis:

• "$\subseteq$":

$a*U=\{\underset{\in G}{\underbrace{a*u}}\mid u\in U\}\subseteq G$

Da jede Nebenklasse eine Teilmenge von $G$ ist, ist auch die Vereinigung der Nebenklassen $\bigcup _{a\in G}a*U$ eine Teilmenge von $G$.

• "$\supseteq$":

Sei $e\in G$ das neutrale Element von $G$.

$\Rightarrow e\in U$, da $U$ die Untergruppe von $G$ ist.

$\tilde{a}=\tilde{a}*e\in \tilde{a}*U$.

Damit ist jedes beliebige $\tilde{a}\in G$ ein Element von $\tilde{a}*U\subseteq \bigcup _{a\in G}a*U=G$.

Damit wissen wir, dass wir $G$ in die Nebenklassen $a*U$ zerlegen können.

• Zerlegung von $G$ in paarweise disjunkte Nebenklassen

Seien $T_a=a*U$ und $T_b=b*U$ mit $a,b\in G$ beliebig gewählte Nebenklassen.

z.z: $T_a\ne T_b\Rightarrow T_a\cap T_b=\mathrm{\varnothing }$

Beweis:

Sei $s\in T_a\cap T_b=(a*U)\cap (b*U)\Rightarrow s\in T_a\wedge s\in T_b\Rightarrow (\mathrm{\exists }{u}_1\in U:s=a*u_1)\wedge (\mathrm{\exists }{u}_2\in U:s=b*u_2)$.

Wir zeigen nun, dass $a*U=b*U$.

• "$\subseteq$":

Sei $u\in U$ beliebig gewählt mit $a*u\in a*U$.

Mit $a*u_1=s=b*u_2$ gilt $a=(b*u_2)*u_1^{-1}=b*(u_2*u_1^{-1})$.

Da $(U,*)$ eine Untergruppe von $(G,*)$ ist, gilt mit $u_1\in U$ auch $u_1^{-1}\in U$.

Ferner gilt auch $u_2*u_1^{-1}\in U$, weil $*$ einen innere Verknüpfung in $(U,*)$.

$a*u=(b*(u_2*u_1^{-1}))*u\stackrel{AGin(G,*)}{=}b*\underset{\in U}{\underbrace{(\underset{\in U}{\underbrace{(u_2*u_1^{-1})}}*\underset{\in U}{\underbrace{u}})}}\in b*U$.

• "$\supseteq$":

Sei $u\in U$ beliebig gewählt mit $b*u\in b*U$.

Mit $a*u_1=s=b*u_2$ gilt $a=(a*u_1)*u_2^{-1}=a*(u_1*u_2^{-1})$.

Analog gilt auch $u_1*u_2^{-1}\in U$ wegen der Untergruppeneigenschaft von $(U,*)$.

$b*u=(a*(u_1*u_2^{-1}))*u\stackrel{AGin(G,*)}{=}a*\underset{\in U}{\underbrace{(\underset{\in U}{\underbrace{(u_1*u_2^{-1})}}*\underset{\in U}{\underbrace{u}})}}\in a*U$.

Insgesamt gilt also $a*U=b*U$, da wir beide Teilmengenbeziehungen $a*U\subseteq b*U$ und $a*U\supseteq b*U$ gezeigt haben.

Insbesondere heißt das für die Nebenklassen $a*U$, dass zwei Nebenklassen entweder gleich oder disjunkt sind.

• Zerlegung von $G$ in paarweise disjunkte gleichmächtige Nebenklassen

Wir definieren eine bijektive Abbildung zwischen $U$ und einer beliebigen Nebenklasse $a*U$:

$\phi :U\to a*U;u\mapsto a*u,a\in G$ beliebig gewählt.

z.z.: $\phi surjektiv\wedge \phi injektiv$

• $\phi surjektiv$:

z.z: $\mathrm{\forall }y\in a*U\mathrm{\exists }x\in U:\phi (x)=y$

Sei $y\in a*U$ beliebig gewählt.

$\Rightarrow \mathrm{\exists }{u}_y\in U:y=a*u_y$

$\Rightarrow \mathrm{\exists }(x:=u_y)wedge(\phi (x)=\phi (u_y)=a*u_y=y)$

• $\phi injektiv$:

z.z: $\mathrm{\forall }{x}_1,x_2\in U:\phi (x_1)=\phi (x_2)\Rightarrow x_1=x_2$

Seien $x_1,x_2\in U$ so gewählt, dass $varphi(x_1)=\phi (x_2)$ gilt.

$\Rightarrow varphi(x_1)=a*x_1=a*x_2=varphi(x_2)$

$\Rightarrow a*x_1=a*x_2$ mit $a\in G$ und $a^{-1}\in G$, da $(G,*)$ Gruppe.

$\Rightarrow a^{-1}*(a*x_1)=a^{-1}*(a*x_2)$

$\stackrel{AG}{\Rightarrow }(a^{-1}*a)*x_1=(a^{-1}*a)*x_2$

$\stackrel{IE}{\Rightarrow }e*x_1=e*x_2$

$\stackrel{NE}{\Rightarrow }{x}_1=x_2$

Also ist $\phi$ auch injektiv.

• Untersuchung der Teilbarkeitseigenschaften

Wir suchen nun ein Repräsentantensystem $V$ für die Faktorgruppe $G/U=\{a*U\mid a\in G\}$.

Für $V$ $(a,b\in V)\wedge (aneqb)\Rightarrow a*U\ne b*U$

$G/U=\{a*U\mid a\in V\}$

Wir benötigen das Repräsentantensystem, damit wir Nebenklassen nicht mehrfach zählen.

• Sei $|G|=\mathrm{\infty }\wedge |U|\ge 1\wedge |U|<\mathrm{\infty }$.

$\Rightarrow |G|=|\bigcup _{a\in V}a*U|=\sum _{a\in V}|a*U|=\sum _{a\in V}|U|=|V|\cdot |U|$.

Mit $|G|=\mathrm{\infty }$ gilt auch $|V|=\mathrm{\infty }$ und somit $|G|=|V|\cdot |U|=\mathrm{\infty }$.

Mit $|G|=\mathrm{\infty }$ und $|U|=\mathrm{\infty }$ gilt insbesondere $|V|\ge 1$, da es mindestens eine Nebenklasse $e*U$ gibt, $e$ neutrales Element in $G$.

Damit gilt auch $|G|=|U|\cdot |V|=\mathrm{\infty }$.

• Für endliche Gruppen gilt:

$k=|G|\ge |U|>1,|G|\ge |V|\ge 1$.

$|G|=|\bigcup _{a\in V}a*U|=\sum _{a\in V}|a*U|=\sum _{a\in V}|U|=|V|\cdot |U|$

$\Rightarrow |U|||G|$.

Satz: RSA-Algorithmus
Sei $m$ eine Klartextnachricht, die mit dem RSA-Algorithmus verschlüsselt wird. Sei $(e,n)$ sei der öffentliche Schlüssel und $(d,n)$ der private Schlüssel. Dann gilt: $m^{e\cdot d}modn\equiv mmodn$
.

Beweis:
z.z.: $m^{e\cdot d}modn\equiv mmodn$.

$m^{e\cdot d}modn$

$\equiv m^{1+k\cdot \phi (n)}modn$
$\equiv m^1\cdot m^{k\cdot \phi (n)}modn$
$\equiv m^1\cdot (m^{\phi (n)}{)}^{k}modn$
$\equiv m\cdot ((m^{Ord(m)}{)}^{\frac{\phi (n)}{Ord(m)}}{)}^{k}modn$
$\equiv m\cdot (1^{\frac{\phi (n)}{Ord(m)}}{)}^{k}modn$
$\equiv m\cdot 1^{k}modn$
$\equiv mmodn$

Grundlegende Definitionen

Definition: Relation

Eine Relation $R$ zwischen zwei Mengen $A$ und $B$ ist eine Teilmenge des kartesischen Produkts $A\times B=\{(a,b)\mid a\in A,b\in B\}:$

$R\subseteq A\times B.$

Definition: Äquivalenzrelation

Eine Äquivalenzrelation auf einer Menge $M$ ist eine Teilmenge $R\subseteq M\times M$, welche folgende Bedingungen erfüllt:

• Reflexivität: Für alle $a\in M$ ist $(a,a)\in R$.
• Symmetrie: Für alle $a,b\in M$, für die $(a,b)\in R$ gilt, ist auch $(b,a)\in R$.
• Transitivität: Für alle $a,b,c\in M$ mit $(a,b)\in R$ und $(b,c)\in R$ gilt, dass auch $(a,c)\in R$.
  

Definition: Äquivalenzklasse

Ist $R$ eine Äquivalenzrelation auf einer Menge $M$, so nennt man für ein $a\in M$ die Teilmenge
$[a{]}_R=\{x\in M\mid (x,a)\in R\}\subseteq M$
die Äquivalenzklasse von $a$ unter der Äquivalenzrelation $R$.

Definition: Teilbarkeit

$a|b\iff \mathrm{\exists }k\in \mathbb{Z}:b=k\cdot a.$

Definition: Kongruenzrelation

Für $a,b\in \mathbb{Z}$ und $m\in \mathbb{N}$ wird definiert:
$a\equiv bmodm:\iff m|(a-b).$

Satz: Kongruenzrelation

Es gilt: $a\equiv bmodm\iff \mathrm{\exists }q\in \mathbb{Z}:a=b+q\cdot m.$

Definition: Restklasse

Es sei $m$ eine von 0 verschiedene ganze Zahl und $a$ eine beliebige ganze Zahl. Die Restklasse von $a$ modulo $m$ ist die Äquivalenzklasse von $a$ bezüglich der Kongruenz modulo $m$, also die Menge der ganzen Zahlen, die bei Division durch $m$ den gleichen Division mit Rest wie $a$ ergeben. Sie besteht somit aus allen ganzen Zahlen $b$, die sich aus $a$ durch die Addition ganzzahliger Vielfacher von $m$ ergeben: $[a{]}_{\equiv }=\{b\mid b=a+km\mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{n}k\in \mathbb{Z}\}=\{b\mid b\equiv a(\mathrm{m}\mathrm{o}\mathrm{d}m)\}$.

Allgemeine Formel für Modulo-Rechnungen

Abbildung Formel_für_Modulo-Rechnen.png

Quellen zu Kryptologie im Schulunterricht

• Schriftliche Ausarbeitung einer Unterrichtsreihe zum Thema Kryptologie (von Mina Ghomi)
• Codes und Verschlüsselungen integrativ im Mathematikunterricht: Vorschlag für ein Curriculum (von Thomas Borys)
• Codierungen im Spiegel der fundamentalen Ideen der Mathematik (von Thomas Borys)
• Welche Vernetzungsmöglichkeiten bietet die Kryptologie? (von Thomas Borys)
• Zauberhogwarts

Lernen durch Autorentätigkeit

Diese Seite entsteht nach dem Prinzip Lernen durch Autorentätigkeit in Wikiversity (siehe Learner being an Author).