Kurs:Gewöhnliche Differentialgleichungen/Einführung in die Einschrittverfahren

Wir widmen uns nun den numerischen Verfahren für die Lösung der Anfangswertaufgaben (1.6) oder der Systeme (1.7). Allgemein basieren die numerischen Lösungsmethoden auf der Diskretisierung (Zerlegung) des Definitionsbereichs der gesuchten Funktion in disjunkte Teilmengen. Gesucht werden diskrete Funktionswerte der gesuchten Funktion, zum Beispiel in den Knoten dieser Zerlegung, also in diskreten Gitterpunkten.

Im Fall einer gewöhnlichen Differentialgleichung wird das Zeitintervall $(t_0,T)$ durch die Gitterpunkte $t_i,i=1,\dots N_h,N_h\in \mathbb{N}$ auf $N_h$ Teilintervalle der Länge $h_i:=t_{i+1}-t_i$, $0<h_i<T-t_0$ geteilt. Die Analyse der numerischen Verfahren wird deutlich vereinfacht, wenn man die Länge der Teilintervalle als konstant betrachtet, $h:=t_{i+1}-t_i$ bezeichnet dann die äquidistante Schrittlänge. Die Menge aller Knoten bildet das Gitter ${\mathrm{G}}_{\mathrm{h}}$, mit $$G_h:=\{t_i=t_0+ih,i=1,\dots N_h\}.(3.1)$$

Ist $y(t)$ die Funktion der exakten Lösung, dann wird die durch die numerische Methode erhaltene Lösung in den Gitterpunkten $t_i,i=1,\dots N_h-1$ eine gewisse Annäherung der exakten Funktion an diesen Stellen sein. In Folgenden wird die numerische Lösung im Gitterpunt $t_i$ als ${\eta }_i$ bezeichnet, $${\eta }_i\approx y(t_i).$$

Im Kapitel 1 haben wir anhand des Beispiels der Uhrkette (Tractrix) den expliziten, siehe (1.2), und den impliziten (1.4) Lösungszugang erklärt. Dabei wurde die Position der Uhr in dem neuen Zeitschritt $t_{i+1}$ entweder durch Projezieren in das gegenwärtige, durch die Uhrkette erzeugte Dreieck mithilfe von gegenwärtigen Werten ${\eta }_i\approx y(t_i)$ bestimmt (explizit), oder die Position der Uhr wurde in die Zukunft projeziert, was zur impliziten Verfahrensvorschrift (1.4) führte. Diese zwei folgenden Lösungsansätze entsprechen den einfachsten numerischen Verfahren für die Differentialgleichung (1.3) für die Uhrkette:

• Explizites Eulerverfahren
  

Für $t=t_{i+1}$ ersetze die Ableitung auf der linken Seite mit dem Rückwärtsdifferenzenquotient, $y^{\prime }(t_{i+1})\approx \frac{y(t_{i+1})-y(t_i)}{h}$, und werte die rechte Seite im alten Zeitpunkt $t_i$ aus. Die ursprüngliche Gleichung $y^{\prime }(t)=f(t,y(t))$ wird dann für $t=t_{i+1}$ durch $$\frac{y(t_{i+1})-y(t_i)}{h}=f(t_i,y(t_i))$$ ersetzt. Diese Gleichung wird aber im Allgemeinen von der exakten Lösung nicht exakt erfüllt. Man sucht nun nach der numerischen Lösung ${\eta }_i$, die die obige approximative Gleichung exakt erfüllt: $$\frac{{\eta }_{i+1}-{\eta }_i}{h}=f(t_i,{\eta }_i)\iff {\eta }_{i+1}={\eta }_i+hf(t_i,{\eta }_i),i=0,\dots N_h-1.(3.2)$$

• Implizites Eulerverfahren
  

Für $t=t_{i+1}$ ersetze die Ableitung auf der linken Seite mit dem Rückwärtsdifferenzenquotient, $y^{\prime }(t_{i+1})\approx \frac{y(t_{i+1})-y(t_i)}{h}$, und werte die rechte Seite in dem neuen Zeitpunkt $t_{i+1}$ aus. Man erhält $$\frac{y(t_{i+1})-y(t_i)}{h}=f(t_{i+1},y(t_{i+1})).$$ Wie oben wird die numerische Lösung ${\eta }_i$ gesucht, die die obige approximative Gleichung exakt erfüllt: $$\frac{{\eta }_{i+1}-{\eta }_i}{h}=f(t_{i+1},{\eta }_{i+1})\iff {\eta }_{i+1}={\eta }_i+hf(t_{i+1},{\eta }_{i+1}),i=1,\dots N_h-1(3.3)$$

Die beschriebenen Gleichungen für das (explixite/implizite) Eulerverfahren (3.2), (3.3) sind durch die Funktion der exakten Lösung $y(t)$ nicht exakt erfüllt, da ein Diskretisierungsfehler durch den Abbruch der Taylor-Entwicklung der Ableitung $y^{\prime }$ entsteht. Durch sukzessives Lösen dieser Gleichungen nach ${\eta }_{i+1}$ erhält man lediglich die numerische Lösung in den Gitterpunkten, ${\eta }_i,i=1,\dots N_h$.

Das Eulerverfahren, aber auch weitere numerische Verfahren kann man mithilfe der Volterra’schen Integralgleichung (2.1) und der numerischen Quadratur erhalten. Ersetzt man das Integral ${\int }_{t_i}^{t_{i+1}}f(s,y(s))ds$ mit der Rechteckregel, siehe Abbildungen 3.1, 3.2, erhält man entweder das explizite oder das implizite Eulerverfahren. Mithilfe der Mittelpunktregel für das Integral, siehe Abbildung 3.3, erhält man das sogenannte verbesserte Eulerverfahren (auch explizite Mittelpunktregel genannt), $${\eta }_{i+1}={\eta }_i+hf(t_{i+\frac{1}{2}},{\eta }_{i+\frac{1}{2}}),\text{wobei}{\eta }_{i+\frac{1}{2}}:={\eta }_i+\frac{h}{2}f(t_i,{\eta }_i).(3.4)$$

In diesem Verfahren wird der Wert der Funktion $f$ in der Mitte zwischen $t_i,t_{i+1}$ (also in $t_{i+\frac{1}{2}}:=\frac{t_i+t_{i+1}}{2}$ und in ${\eta }_{i+\frac{1}{2}}\approx y(t_{i+\frac{1}{2}})$) verwendet. Hier wird zur Approximation des Wertes im Mittelpunkt, $y(t_{i+\frac{1}{2}})$, ein Schritt des expliziten Eulerverfahrens mit der halben Schrittlänge $\frac{h}{2}$ benutzt.

Durch die Trapezregel für die numerische Integration, siehe Abbildung 3.4, erhält man folgendes Verfahren, welches auch implizite Trapezregel heißt: $${\eta }_{i+1}={\eta }_i+\frac{h}{2}(f(t_i,{\eta }_i)+f(t_{i+1},{\eta }_{i+1})).(3.5)$$

In der expliziten Variante dieses Verfahrens würde man $f(t_{i+1},{\eta }_{i+1})$ mithilfe eines Schrittes des Eulerverfahrens mit $f(t_{i+1},{\eta }_i+hf(t_i,{\eta }_i))$ ersetzen.
Mithilfe der Mittelpunktsregel, erhält man folgendes Verfahren, welches auch
implizite Mittelpunktregel heißt: $${\eta }_{i+1}={\eta }_i+hf(t_{i+1/2},\frac{{\eta }_i+{\eta }_{i+1}}{2}).(3.6)$$

In der expliziten Variante würde man $\frac{{\eta }_i+{\eta }_{i+1}}{2}$ durch einen halben Schritt des expliziten Eulerverfahrens mit ${\eta }_i+\frac{h}{2}f(t_i,{\eta }_i)$ ersetzen, siehe (3.6).

Abbildung 3.1: Explizite Rechteckregel zur Approximation des Integrals $I[f(x)]={\int }_a^{b}f(x)dx$ mit einem Quadraturknoten $x_0=a$.

Abbildung 3.2: Implizite Rechteckregel zur Approximation des Integrals $I[f(x)]={\int }_a^{b}f(x)dx$ mit einem Quadraturknoten $x_0=b$.

Die eben beschriebenen numerischen Lösungsansätze benötigen für die Berechnung des Funktionswertes im neuen Gitterpunkt $t_{i+1}$ nur den vorherigen Wert aus $t_i$. Solche Verfahren nennen wir Einschrittverfahren (ESV). Die Mehrschrittverfahren (MSV) dagegen nutzen auch die Information von mehreren vorherigen Schritten $t_i,t_{i-1},\dots ,t_{i-k+1}$, wobei $k$ hier fest ist (k-Schrittverfahren).

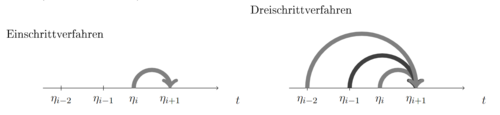
Abbildungen Einschrittverfahren und Dreischrittverfahren.

In diesem Kapitel werden wir numerische Lösungsformeln für die Einschrittverfahren und deren Diskretisierungsfehler untersuchen. Dabei werden nur die numerischen Verfahren in Frage kommen, die die exakte Lösung ausreichend gut annähern.

Abbildung 3.3: Mittelpunktregel zur Approximation des Integrals $I[f(x)]={\int }_a^{b}f(x)dx$ mit einem Knoten $x_0=\frac{a+b}{2}$.

---

Definition 3.1 (Explizites Einschnittsverfahren (ESV))

Gegeben sei die äquidistante Schrittlänge $0<h\le T-t_0$, das Gitter $G_h$, siehe (3.1). Das explizite Einschrittverfahren ist beschrieben durch folgende iterative Vorschrift, $${\eta }_{i+1}={\eta }_i+h\mathrm{\Phi }(t_i,{\eta }_i;h;f),i=0,\dots ,N_h-1,$$ Gleichung (3.7)

wobei $\mathrm{\Phi }(\cdot ,\cdot ;h;f):\{G_h-t_{N_h}\}\times {ℝ}^m\to {ℝ}^m$ die Verfahrensfunktion heißt.

---

Beispiel 3.1

Die Verfahrensfunktion für das explizite Eulerverfahren ist $$\mathrm{\Phi }(t,y;h;f)=f(t,y),$$ und für das verbesserte (modifizierte) Eulerverfahren (3.4) $$\mathrm{\Phi }(t,y;h;f)=f(t+\frac{h}{2},y+\frac{h}{2}f(t,y)).$$ $\diamond$

Abbildung 3.4: Trapezregel zur Approximation des Integrals $I[f(x)]={\int }_a^{b}f(x)dx$ mit zwei Knoten $x_0=a,x_1=b.$

Beispiel 3.2

Wir lösen die einfache Anfangswertaufgabe $y^{\prime }=y,y(0)=1$ mit explizitem Eulerverfahren mit konstanter Schrittweite $h=\frac{T}{N_h}$.
Die numerische Lösung ist: $$\begin{array}{ccc}{\eta }_0& =& 1,\\ {\eta }_1& =& 1+hf(t_0,{\eta }_0)=1+h{\eta }_0\\ & =& 1+h,\\ {\eta }_2& =& {\eta }_1+hf(t_1,{\eta }_1)=1+h+h{\eta }_1\\ & =& 1+h+h(1+h)=(1+h{)}^2,\\ {\eta }_3& =& {\eta }_2+hf(t_2,{\eta }_2)\\ & =& (1+h{)}^2+h{\eta }_2=(1+h{)}^3,\\ & \dots & \end{array}$$

Mit mathematischer Induktion kann man zeigen, dass ${\eta }_i=(1+h{)}^i,i=1,\dots N_h$. Daraus folgt, dass ${\eta }_{N_h}=(1+\frac{T}{N_h}{)}^{N_h}$ gegen $e^T$ für $N_h\to \mathrm{\infty }$ konvergiert. Dies entspricht der exakten Lösung $y(T)$. Also konvergiert die numerische Lösung in einem bestimmten Zeitpunkt $t=T$ gegen die exakte Lösung in diesem Zeitpunkt für Schrittweite $h$ gegen Null. $\diamond$