Maschinelles Lernen

Einführung

Maschinelles Lernen (ML) ist ein Oberbegriff für die „künstliche“ Generierung von Wissen aus Erfahrung: Ein künstliches System lernt aus Beispielen und kann diese nach Beendigung der Lernphase verallgemeinern.

Lerneinheiten

Lerneinheiten gliedern sich die Betrachtung von

Klassen maschinellen Lernens
Lernalgorithmen und Lernregeln

Klassen maschinellen Lernens

/überwachtes Lernen/
/unüberwachtes Lernen/

Trainingsdaten / Testdaten

Beim maschinellen Lernen unterscheidet man

/Trainingsdaten/ und
/Testdaten/ (Validierungsdatensätze).

Lernalgorithmen und Lernregeln

/Hebbsche Lernregel/
Koaktivitätsmatrix - (Foliensatz)

Zeitliche Veränderung eines Systems

In dem Begriff "Maschinelles Lernen" eines System $M$ steckt bereits eine zeitliche Veränderung des Systems in der Zeit. In der folgenden Lernressource wird daher ein Maschinelles Lernsystem (kurz ML-System) $M_{t}$ mit einem Zeitindex $t$ versehen, das den Zustand des ML-Systems $M$ zum Zeitpunkt $t$ .

Maschinelles Lernen als Funktionenfolge

In dieser Lernressource wird Maschinelles Lernen (ML) als eine Funktionenfolge $(M_{t})_{t \in R}$ betrachtet, das sich in der Zeit $t$ verändert. $M_{t} : X \to Y$ ist zu jedem Zeitpunkt $t \in T$ eine Abbildung von einem Definitionsbereich $X$ in den Wertebereich $Y$ .

Verallgemeinerungsfähigkeit

Ein künstliches System, das aus Beispielen lernt, kann "verallgemeinern", wenn nicht nur für die Trainingsdaten (z.B. Ein-Ausgabepaare $(x_{i}, y_{i}) \in 𝔻 \subset X \times Y$ aus dem Ein-Ausgabegrundraum) korrekt Ausgaben produziert werden, sondern auch für neue unbekannte Eingaben korrekte bzw. akzeptabel gute Ausgaben produziert werden.

Überwachtes Lernen

Wenn man Ein-Ausgabepaare $(x_{i}, y_{i}) \in 𝔻 \subset X \times Y$ als Trainingsdaten verwendet, spricht man von überwachtem Lernen. Die $y_{i} \in Y$ entspricht den erwarteten/empfohlenen Ausgaben einer "lehrenden" bzw. trainierenden Instanz. In der Trainingsphase bekommt das System $M$ Daten der Form der Ein-Ausgabepaare $(x_{i}, y_{i})$ und in der Testphase.

Unüberwachtes Lernen

Wenn man lediglich Eingaben $x_{i} \in X$ eine System als Trainingsdaten verwendet, spricht man von unüberwachtem Lernen. Die $y_{i} \in Y$ entspricht den erwarteten/empfohlenen Ausgaben einer "lehrenden" bzw. trainierenden Instanz.

Bestärkendes Lernen

Vorlage:Hauptartikel Das bestärkende Lernen ist ein Bereich des maschinellen Lernens, der sich mit der Frage beschäftigt, wie Agenten in einer Umgebung agieren sollten, um einen bestimmten Wert der kumulierten Belohnung zu maximieren.^[1]^[2] Aufgrund seiner Allgemeingültigkeit wird dieses Gebiet auch in vielen anderen Disziplinen untersucht, z. B. in der Spieltheorie, der Kontrolltheorie, dem Operations Research, der Informationstheorie, der simulationsbasierten Optimierung, den Multiagentensystemen, der Schwarmintelligenz, der Statistik und den genetischen Algorithmen. Beim maschinellen Lernen wird die Umgebung normalerweise als Markov-Entscheidungsprozess (MDP) dargestellt. Viele Algorithmen des Verstärkungslernens verwenden Techniken der dynamischen Programmierung.^[3] Verstärkungslernalgorithmen setzen keine Kenntnis eines exakten mathematischen Modells des MDP voraus und werden eingesetzt, wenn exakte Modelle nicht durchführbar sind. Verstärkungslernalgorithmen werden in autonomen Fahrzeugen oder beim Lernen eines Spiels gegen einen menschlichen Gegner eingesetzt.

Fehler und deren Optimierung durch Lernen

Zunächst einmal ist die Quantifzierung von Fehlern ein wesentliches Merkmal numerischer Ansätze für die Optimierung von Systemen. Dazu benötigt man grundlegende Definitionen einer Abweichung von Trainingsdaten.

Fehlermaße

Normen, Metriken, Topologie

In der Mathematik liefern Normen, Metriken oder Gaugefunktionale in der Topologie Messinstrumenten, um auf gegeben Räumen Fehler oder Abweichungen zu messen.

Definition - Metrischer Ausgabefehler für Maschinelles Lernen

Sei $(M_{t})_{t \in T}$ ein maschineller Lernprozess und $(Y, d_{Y})$ ein metrischer Raum. Ein Augabefehler zum Zeitpunkt $t \in T$ für die Eingabe $x \in X$ für ein zugehöriges Trainingsdatum $(x, y) \in X \times Y$ ist als metrischer Abstand $d_{Y} (M_{t} (x), y)$ definiert.

Bemerkung - Metrischer Ausgabefehler für Maschinelles Lernen

Mit dem Abstand $d_{Y} (M_{t} (x), y)$ zwischen der zum Zeitpunkt $t \in T$ generierten Ausgabe $M_{t} (x)$ zu $x$ wird die Distanz zum Sollwert $y \in Y$ gemessen. Das lernenden System $(M_{t})_{t \in T}$ verändert seine Ausgabeverhalten mit der Zeit. Der Ausgabefehler für $x$ wird zwischen $t_{1} < t_{2}$ kleiner, wenn gilt:

d_{Y} (M_{t_{1}} (x), y) > d_{Y} (M_{t_{2}} (x), y)

Dies bedeutet, dass der Abstand zum Sollwert $y$ zu einem späteren Zeitpunkt $t_{2}$ sich verbessert hat.

Optimierung des metrischen Ausgabefehler für Maschinelles Lernen

Die metrische Optimierung des Ausgabefehlers erfolgt aber nicht für einen singulären Eingabewert $x \in X$ bzw. für ein Ein-Ausgabepaar $(x, y) \in X \times Y$ , sondern in der Regel für eine endliche Testmenge $𝔻_{1} : = {(x_{i}, y_{i}) \in X \times Y : i \in {1, . . ., n}}$ mit $n \in ℕ$ . Die Ein-Ausgabepaare $𝔻_{1} \subset X \times Y$ verwendet man dabei nicht für das Training des Maschinellen Lernsystems $M : = (M_{t})_{t \in T}$ , sondern für der Test der Güte der Ausgabe von $M$ bei unbekannten Ein-Ausgabepaaren aus $𝔻_{1}$ .

Definition - Metrischer Fehlervektor für Maschinelles Lernen

Sei $(M_{t})_{t \in T}$ ein maschineller Lernprozess und $(Y, d_{Y})$ ein metrischer Raum. Ein metrischer (Augabe-)Fehlervektor zum Zeitpunkt $t \in T$ für eine endliche Testmenge $𝔻_{1} : = {(x_{i}, y_{i}) \in X \times Y : i \in {1, . . ., n}}$ mit $n \in ℕ$ ist ein Vektor

e : = (e_{1}, . . ., e_{n}) : = (d_{Y} (M_{t} (x_{1}), y_{1}), . . ., d_{Y} (M_{t} (x_{n}), y_{n}) \in ℝ^{n}

definiert.

Definition - Fehlervektornorm für Maschinelles Lernen

Sei $c_{o o} (ℝ)$ der Raum der endlichen Folgen in $ℝ$ und $‖ \cdot ‖ : c_{o o} (ℝ) \to ℝ_{0}^{+}$ eine Norm auf $c_{o o} (ℝ)$ . Ferner sei ein Fehlervektor eines Maschinellen Lernprozesses $(M_{t})_{t \in T}$ gegeben.

e : = (e_{1}, . . ., e_{n}) : = (d_{Y} (M_{t} (x_{1}), y_{1}), . . ., d_{Y} (M_{t} (x_{n}), y_{n}) \in ℝ^{n}

definiert. Die Fehlervektornorm von $e$ ist dann $‖ \hat{e} ‖$ mit $\hat{e} : = (e_{n}, . . ., e_{1}, 0, 0, 0, . . . .) \in c_{o o} (ℝ)$ .

Bemerkung - Fehlervektornorm für Maschinelles Lernen

Eine Norm $‖ \cdot ‖ : V \to ℝ_{0}^{+}$ ist auf einem Vektorraum $V$ definiert. Die Fehlervektornorm muss für unterschiedliche Trainingsdatenlängen definiert sein. Daher bettet man die Fehlervektoren $e : = (e_{1}, . . ., e_{n}) \in ℝ^{n}$ in umgekehrter Reihenfolge in den Folgenraum $V : = c_{o o} (ℝ)$ ein.

Bemerkung - Neue Trainingsdaten für Maschinelles Lernen

Wird ein neues Ein-Ausgabepaar $(x_{n + 1}, y_{n + 1}) \in X \times Y$ zum Testdatensatz $\hat{e_{n}} : = (e_{n}, . . ., e_{1}, 0, 0, 0, . . . .) \in c_{o o} (ℝ)$ ergänzt, so ergibt sich: $\hat{e_{n + 1}} : = (e_{n + 1}, e_{n}, . . ., e_{1}, 0, 0, 0, . . . .) \in c_{o o} (ℝ)$ Die Ergänzung von links ist hilfreich, um die Alterung von Daten bei einem Rechtsshift der Einträge innerhalb der Norm zu kodieren.

Alterung von Daten - erste Schritte

Für die Alterung von Daten betrachten man zunächst erste Schritte, die dann zu Verallgemeinerungen führen, die mit einem Skalarprodukt auf Folgenräumen ausgedrückt werden können. Zunächst einmal sollen aktuelle Daten mit einem Faktor 1 gewichtet werden und qualitativ bei älteren Daten die Gewichtung gegen 0 konvergieren. Dazu betrachten wir eine monoton fallende Alterungsfolge in $w : = (w_{n})_{n \in ℕ} \in ℓ_{2} (ℝ_{0}^{+})$ (siehe Folgenräume).

Beispiel - Alterung von Daten

$w : = (w_{n})_{n \in ℕ} : = {(\frac{1}{n})}_{n \in ℕ} \in ℓ_{2} (ℝ_{0}^{+})$ definiert eine Alterung auf den Daten.

Trainings- und Testdaten mit Zeitstempel

Als Trainingsdaten betrachtet man Ein-Ausgabepaare $(x_{i}, y_{i}, t_{i}) \in 𝔻 \subset X \times Y \times T$ aus dem Kartesischen Produkt Ein-Ausgabegrundraum und der Zeitmenge $T$ . Der zusätzlich Zeitstempel für Trainingsdaten ist nun dann notwendig, wenn man das Alter der Trainingsdaten im Lernprozess berücksichtigen möchten. Ansonsten wählt man Trainings- und Testdaten für den maschinellen Lernprozess aus $X \times Y$ .

Bemerkung - Überwachtes Lernen

In dem obigen Annahmen geht man davon aus, dass ein überwachtes maschinelles Lernen verwendet wird und damit Sollwerte $y_{i} \in Y$ zu Eingabewerten $x_{i} \in X$ . In einem unüberwachten Lernprozess bestehen die Trainingsdaten nur aus Daten $x_{i} \in X$ . Die wird auch ein Kriterium sein, überwachtes und unüberwachtes Lernen bzgl. machinellen Lernalgorithmen $L$ zu unterscheiden.

Änderung der Wichtung über die Zeit

Wenn die Alterung von Trainingsdaten beim maschinellen Lernprozess berücksichtigt werden, kann man die Wichtung dynamisch bzgl. der aktuellen Zeit berechnen. Eine mögliche Option wäre bei einem aktuellen Zeitpunkt $t \in T \subset ℝ$ mit $s > 0$ und $i \leq n$ :

w_{i} : = \frac{1}{1 + \frac{(t - t_{i})^{2}}{s}}

Für $i > n$ setzt man $w_{i} = 0$ . In dem obigen Term bestimmt $s > 0$ , wie stark die Wichtung mit wachsendem Alter gegen 0 konvergiert.

Vorteil bzgl. Umordnung der Trainings- bzw. Testdaten

Mit einem berechneten Wichtungsvektors $w = (w_{i})_{i \in ℕ}$ aus dem Alter der Trainingsdaten entfällt die Umordung. Insbesondere beim Online-Learning, bei dem kontinuierlich neue Trainingsdaten im Lernprozess z.B. eines künstlichen neuronalen Netzes berücksichtigt werden.

Aufgabe - Fehlervektornorm für Maschinelles Lernen

Definieren Sie eine Fehlernorm auf $c_{o o} (ℝ)$ , die den Fehler bei älteren Daten weniger stark gewichtet! Welche Eigenschaften sollten die Wichtungen der Fehlernorm aufweisen?

Beispiel - lernfähiger Fuzzy-Controller

Betrachten Sie einen lernfähigen Fuzzy-Controller für eine Klimaanlage, der aus dem Regelungsverhalten der Personen im Raum erlernt, wann es den Personen zu warm oder zu kalt ist.

$X : = [a, b]$ mit $a : = - 20$ und $b : = 50$ als Temperaturintervall.
$Y : = [0, 1]$ ist das Regelungsintervall am Heizkörper. 0 entspricht geschlossen und 1 entspricht der wärmsten Einstellung am Regler.

Diskrete Trainingsdaten

Wählen Sie in einer Tabellenkalkulation diskrete Trainingsdaten $(x_{i}, y_{i}) \in X \times Y$ und rekonstruieren Sie daraus die Zugehörigskeitsfunktion für einen Fuzzy-Controller, der beschreibt, wann eine Temperatur für die Person in dem Raum angenehm ist.

Aufgabe - Optimierung bzgl. Nachhaltigkeit

Klimaanlagen benötigen viel Energie. Wie kann man das Regelungsverhalten optimieren, wenn man gleichzeitig weiß, wie viele Personen sich in einem Raum über den Tag bzw. im zeitlichen Verlauf befinden? Benennen Sie zunächst die Voraussetzung für den Definitionsbereich $X$ , wenn weitere inhaltliche Aspekte mit der Fuzzy-Zugehörigkeitsfunktion repräsentiert werden sollen! Welche fuzzy-logischen Operationen sind dafür notwendig.

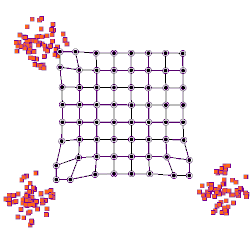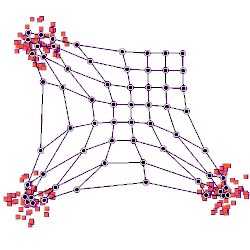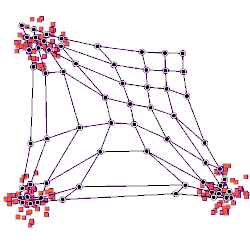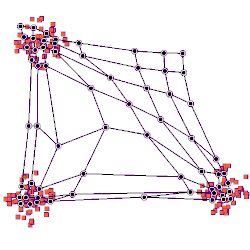
Animation eines Lernprozesses

Mathematisches Grundkonzept für das Maschinelle Lernen

Dazu basieren Algorithmen beim maschinellen Lernen auf einem statistischen oder numerischen Modell, das mit Trainingsdaten "gefüttert" und ggf. mit Testdaten auf Güte getestet wird.

Mustererkennung - Erkennung von Gesetzmäßigkeiten

Beim maschinellen Lernen werden nicht einfach die Beispiele auswendig gelernt, sondern Muster und Gesetzmäßigkeiten sollen in den Lerndaten erkannt werden, damit durch die Lernphase diese Gesetzmäßigkeiten von dem System auch unbekannte Eingabedaten angewendet werden kann (siehe auch Lerntransfer).

Überanpassung - Overfitting

In der Regel wird durch das Maschinelle Lernen das lernfähige System auf den Trainingsdaten immer besser. Dieser Verbesserung wird z.B. durch numerische Verfahren, wie dem Gradientenabstiegsverfahren) generiert, mit dem man eine Fehlerfunktion schrittweise weiter minimiert. Dabei tritt das Phänomen der Überanpassung) auf.

Trainingsdaten

Auf den Trainingsdaten, die das lernfähige System für den maschinellen Lernprozess erhält, werden die Fehler in der Ausgabe geringer.

Testdaten

Auf den Testdaten, die das lernfähige System für den maschinellen Lernprozess keinen Zugriff. Die Testdaten dienen der Überprüfung der "Verallgemeinerungsfähigkeit" des lernfähigen Systems. Werden die Fehler in der Ausgabe nach einer gewissen Trainingszeit auf der Testmenge wieder signifikant schlechter, spricht man vom einer Überanpassung (engl. overfitting).^[4]^[5]

Anwendungen

Aus dem weiten Spektrum möglicher Anwendungen seien hier genannt:

Sprach- und Texterkennung,
Intelligente Tutorielle Systeme (ITS) und Digitale Lernumgebungen
automatisierte Diagnoseverfahren und autonome Systeme.
Erkennung von Kreditkartenbetrug und Aktienmarktanalysen,
Klassifikation von Nukleotidsequenzen.

Zusammenhang - Data Mining und Knowledge Discovery

Das Thema ist eng verwandt mit „Knowledge Discovery in Databases“ und „Data-Mining“, bei dem es jedoch vorwiegend um das Finden von neuen Mustern und Gesetzmäßigkeiten geht. Viele Algorithmen können für beide Zwecke verwendet werden.

Von Knowledge Discovery zu Maschinellem Lernen

Methoden der „Knowledge Discovery in Databases“ können genutzt werden, um Lerndaten für „maschinelles Lernen“ zu produzieren oder vorzuverarbeiten. Die Qualtität der Ausgaben von lernfähigen Systemen hängt maßgeblich von der Qualtiät der Trainingsdaten ab. Daher können Methoden der Erkennung von Wissens zur Qualitätsverbesserung der Ausgaben vom lernfähigen Systemen beitragen.

Maschinelles Lernen für Data Mining

Die Herausforderung in heutiger Zeit ist es, aus großen Wissen und Entscheidungsunterstützung abzuleiten. Wachsen die Datenmengen wird der Rechenaufwand größer und damit kommt man an Grenzen, in akzeptabler Zeit einen großen Suchraum zu analysieren. Hauptziel dabei ist es, einerseits den Berechnungsaufwand in einer Weise zu reduzieren, der andererseits keinen zu großen Einfluss auf die Güte der Ergebnisse hat. Also mit weniger Suchaufwand nahezu die gleiche Güte der Suchergebnisse zu behalten.

Symbolische und nicht-symbolische Ansätze

Beim maschinellen Lernen spielen Art und Mächtigkeit der Wissensrepräsentation eine wichtige Rolle. Man unterscheidet zwischen symbolischen Ansätzen und nicht-symbolischen Ansätzen.

Symbolische Ansätze

Bei symbolischen Ansätzen wird das Wissen – sowohl die Beispiele als auch die induzierten Regeln – explizit repräsentiert ist. Diese Regelsystemen können z.B. Fuzzy-Regelsysteme, bei denen die Gültigkeit einer Regel oder eines linguistischen Wertes durch einen maschinellen Lernprozess festgelegt werden.

Ein Spezialfall der Fuzzylogik sind symbolischen Ansätzen aus der AussagenlogikB und Prädikatenlogil. Vertreter der ersteren sind ID3 und sein Nachfolger C4.5. Letztere werden im Bereich der induktiven logischen Programmierung entwickelt.

Statistische Inferenz

Das Schließen von Daten auf (hypothetische) Modelle wird als Statistische Inferenz bezeichnet.

Nicht-symbolische Ansätze

Bei nicht-symbolischen Ansätzen, wie z.B. neuronalen Netzen, wird durch einen maschinellen Lernprozess ein berechenbares Verhalten „antrainiert“. Dabei geht es um eine möglichst gute Vorhersage von einem Systemverhalten durch das lernfähige System. Gütekriterium ist dabei die Vorhersagegüte. Dieses Vorgehen erlaubt jedoch keinen Einblick in die erlernten Lösungswege und ggf. vorhandene interne Regelsystem, das das Verhalten bestimmt. In einem solchen Fall wird das Wissen implizit repräsentiert.^[6]

Deep Learning

Zu unterscheiden ist der Begriff zudem von dem Begriff „Deep Learning“, welches nur eine mögliche Lernvariante mittels künstlicher neuronaler Netze darstellt.

Hybride Ansätze

Bei hybdriden Ansätzen des maschinellen Lernens werden symbolische und nicht-symbolische Ansätze miteinander verbunden. Dies kann beispielsweise durch Neuro-Fuzzy-Systeme^[7] erfolgen, bei denen die symbolische Ansätze durch Fuzzy-Regelsysteme abgedeckt werden und die nicht-symbolischen Ansätze durch neuronale Netze.

Algorithmische Ansätze

Die praktische Umsetzung geschieht mittels Algorithmen. Verschiedene Algorithmen aus dem Bereich des maschinellen Lernens lassen sich grob in drei Gruppen einteilen:^[8] überwachtes Lernen (englisch supervised learning), unüberwachtes Lernen (englisch unsupervised learning) und bestärkendes Lernen (engl. reinforcement learning).

Automatisches Maschinelles Lernen

Vorlage:Hauptartikel Automatisches maschinelles Lernen automatisiert viele Schritte des maschinellen Lernens.

Literatur

Sebastian Raschka, Vahid Mirjalili (2017) Machine Learning mit Python und Scikit-Learn und TensorFlow: Das umfassende Praxis-Handbuch für Data Science, Predictive Analytics und Deep Learning URL: https://books.google.com/books?id=JM5CDwAAQBAJ - Date: 13. Dezember 2017, MITP-Verlags GmbH & Co. KG, 978-3-95845-735-5
Vorlage:Literatur
Vorlage:Literatur
Vorlage:Literatur
Vorlage:Literatur
Vorlage:Literatur
Vorlage:Literatur
Vorlage:Literatur
Vorlage:Literatur
Arthur L. Samuel (1959): Some studies in machine learning using the game of checkers. IBM J Res Dev 3:210–229. doi:10.1147/rd.33.0210.
Alexander L. Fradkov: Early History of Machine Learning. IFAC-PapersOnLine, Volume 53, Issue 2, 2020, Pages 1385-1390, doi:10.1016/j.ifacol.2020.12.1888.

Weblinks

Vorlage:Internetquelle
Vorlage:Internetquelle
golem.de, Miroslav Stimac: So steigen Entwickler in Machine Learning ein, 12. November 2018
Introduction to Machine Learning (englisch)
Maschinen lernen – ohne Verstand ans Ziel, Wissenschaftsfeature, Deutschlandfunk, 10. April 2016. Audio, Manuskript

Siehe auch

Vorlage:Commonscat

Einzelnachweise

↑ Vorlage:Literatur
↑ Vorlage:Internetquelle
↑ Vorlage:Literatur
↑ Vorlage:Literatur
↑ Vorlage:Literatur
↑ Vorlage:Literatur
↑ Kar, S., Das, S., & Ghosh, P. K. (2014). Applications of neuro fuzzy systems: A brief review and future outline. Applied Soft Computing, 15, 243-259.
↑ ftp://ftp.sas.com/pub/neural/FAQ.html#questions

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Maßtheorie auf topologischen Räumen' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Maschinelles%20Lernen
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

Wikipedia2Wikiversity

Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:

[1] Vorlage:Literatur

[2] Vorlage:Internetquelle

[3] Vorlage:Literatur

[4] Vorlage:Literatur

[5] Vorlage:Literatur

[6] Vorlage:Literatur

[7] Kar, S., Das, S., & Ghosh, P. K. (2014). Applications of neuro fuzzy systems: A brief review and future outline. Applied Soft Computing, 15, 243-259.

[8] tp://ftp.sas.com/pub/neural/FAQ.html#questions

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]