Kurs:Mathematische Modellbildung/Lehrerbedarf/Modellierungszyklus 3

Einführung

In Modellierungszyklus 2 wurde die Zahl der Lehrkräfte 2026 ermittelt
Um eine konkrete Aussage über den Lehrerbedarf 2026 treffen zu können, wird die Schülerzahl für das Jahr 2026 benötigt
Fokus liegt auf der Schülerzahl in der Sekundarstufe 1 in Rheinland-Pfalz

Inhaltliche Beschreibung

Schülerzahl

Annahme: Die Schüler in der Sekundarstufe 1 sind zwischen 10 und 15 Jahren alt.

Die Schülerzahl 2026 setzt sich daher aus den folgenden Punkten zusammen:

Geburtenzahlen von 2011-2016 in Rheinland-Pfalz
Kinder im Alter von 10 bis 15 Jahren, die zwischen 2020 und 2026 nach Rheinland-Pfalz wandern werden
Kinder im Alter von 4 bis 9 Jahren, die bis 2020 nach Rheinland-Pfalz gewandert sind

Migration

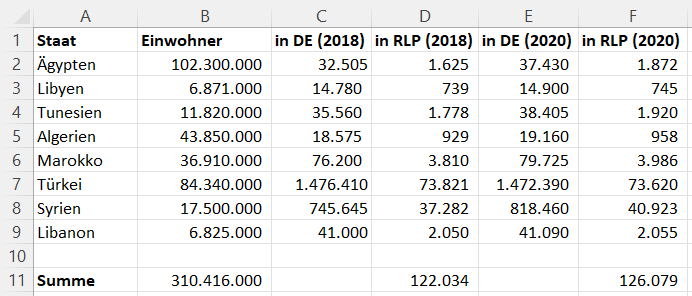
Bei der Migration werden folgende Herkunftsländer betrachtet:

Ägypten, Libyen, Tunesien, Algerien, Marokko, Libanon, Syrien, Türkei

Mathematisches Modell

Geburtenzahlen 2011-2016

0,4% Kindersterblichkeit in Deutschland ^[1]
Schulpflicht in Deutschland bzw. Rheinland-Pfalz
Die Zahl der Einschulungen in einem Jahr $t$ ergibt sich aus der Zahl der Geburten im Jahr $t - 10$ mal 0,996

Migration zwischen 2020 und 2026

Zahl der Migranten in Deutschland bekannt ^[2]
5 Prozent der in Deutschland erfassten Migranten leben in Rheinland-Pfalz ^[3]

Implementation der Migranten 2018 & 2020 in Excel

Lineare Regression

Mithilfe der linearen Regression als Werkzeug könnten die ermittelten Wertepaare approximiert werden
Unter Berücksichtigung der Werte von 2018 bis 2020 ergibt sich die Funktionsvorschrift: $f (x) = - 3.959.252, 835 + 2022, 5 \cdot x$
Ansatz kann verworfen werden, da lineare Funktionen nicht konvergieren und somit gegen keine Sättigungsgrenze steuern
In der Realität erreicht die Migration aber eine obere Schranke, da nicht mehr Menschen aus einem Land auswandern können, als das Land Einwohner hat

Logistisches Wachstum

Stattdessen zunächst exponentieller Anstieg der Migrantenzahlen erwartet, die dann in ein beschränktes Wachstum übergehen
Dieser Zusammenhang kann mit dem logistischen Wachstum beschrieben werden
$f (t) = \frac{f (0) \cdot S}{f (0) + (S - f (0)) \cdot e^{- S \cdot k \cdot t}}$
Jahr 2018 entspricht $t = 0$
$f (0) = 122.034$ (aus Tabelle)

Bestimmung der Sättigungsgrenze S

Einwohner in den Herkunftsländern: 310.416.000
Annahme: höchstens 20% wandern nach Deutschland
5 Prozent der in Deutschland erfassten Migranten leben in Rheinland-Pfalz
Zusammen: $S = 310.416.000 \cdot 0, 2 \cdot 0, 05 = 3.104.160$

Bestimmung der Wachstumskonstante k

Jahr 2018 entspricht $t = 0$ ⇒ Jahr 2020 entspricht $t = 2$
$f (2) = 126.079$ (aus Tabelle)
in Formel für das logistische Wachstum einsetzen: $126.079 = \frac{122.034 \cdot 3.104.160}{122.034 + (3.104.160 - 122.034) \cdot e^{- 3.104.160 \cdot k \cdot 2}}$
nach k auflösen
$k \approx 5, 4711 \cdot 1 0^{- 9}$
Allgemein ergibt sich nun folgende Gleichung: $f (t) = \frac{122.034 \cdot 3.104.160}{122.034 + (3.104.160 - 122.034) \cdot e^{- 3.104.160 \cdot 5, 4711 \cdot 1 0^{- 9} \cdot t}}$

Zur Bestimmung der Zahl der Migranten, die sich 2026 in Rheinland-Pfalz befinden, wird nun $t = 8$ in $f$ eingesetzt
$f (8) = \frac{122.034 \cdot 3.104.160}{122.034 + (3.104.160 - 122.034) \cdot e^{- 3.104.160 \cdot 5, 4711 \cdot 1 0^{- 9} \cdot 8}} = 138.998, 0903$
Somit leben im Jahr 2026 138.998 Migranten in Rheinland-Pfalz
Nun ist von Interesse, wie viele Menschen zwischen 2020 und 2026 hinzu gekommen sind
Differenz: $138.998 - 126.079 = 12.919$
Also: 12.919 Menschen von 2020-2026 nach Rheinland-Pfalz gewandert

Kinder zwischen 10 und 15 Jahren

Anteil der 10- bis 14-Jährigen und 15- bis 19-Jährigen aus den Bevölkerungspyramiden der Länder entnommen^[4]
Anteil der 15-Jährigen aus dem Anteil der 15- bis 19-Jährigen bestimmt (Annahme einer Gleichverteilung, daher ein Fünftel)

Implementation Anteile der Migranten in Excel

Unter den 12.919 Menschen, die zwischen 2020 und 2026 nach Rheinland-Pfalz wandern werden, sind 1.323 Kinder zwischen 10 und 15 Jahren
Denn es gilt: $12.919 \cdot 0, 1224 = 1.322, 9056$

Migration bis 2020

Betrachtung der Kinder, die nicht in Deutschland geboren sind und bis 2020 nach Rheinland-Pfalz gewandert sind
4- bis 9-Jährige, da sich diese Kinder im Jahr 2026 in der Sekundarstufe 1 befinden
analoge Argumentation/Rechnung

Zwischenfazit

Alle ermittelten Werte werden addiert
$199.329 + 1.323 + 13.427 = 214.079$
Ergebnis gibt Schülerzahl 2026 an

Vergleich 2022

Geburtenzahlen 2007-2012

Zur Bestimmung der Migranten, die sich 2022 in Rheinland-Pfalz befinden, wird $t = 4$ in $f$ eingesetzt
Es gilt: $f (4) = 130.252, 2223$
Differenz zwischen den Jahren 2022 und 2020: $130.252 - 126.079 = 4.173$
Somit sind 4.173 Menschen in den zwei Jahren nach Rheinland-Pfalz gewandert
Darunter sind 427 Kinder zwischen 10 und 15 Jahren, da $4173 \cdot 0, 1024 = 427, 3152$

Betrachtung der Kinder zwischen 8 und 13 Jahren, die bereits vor 2020 nach Rheinland-Pfalz gewandert sind

Alle Werte addieren: $188.706 + 427 + 13.228 = 202.361$
Ergebnis gibt Schülerzahl 2022 an

Software: Tabellenkalkulation

Einwohnerzahl der Herkunftsländer und Migrantenzahl in Deutschland bekannt
Migrantenzahl in Rheinland-Pfalz soll bestimmt werden
(D2) Befehl für die Migranten aus Ägypten in RLP (2018): =RUNDEN(0,05*C2;0)
(F2) Befehl für die Migranten aus Ägypten in RLP (2020): =RUNDEN(0,05*E2;0)
alle weiteren Länder analog
(D11), (F11) Summe der in Rheinland-Pfalz lebenden Migranten über den Befehl: =SUMME(D2:D9) bzw. =SUMME(F2:F9)

Anteil der 10- bis 14-Jährigen und 15- bis 19-Jährigen aus den Bevölkerungsdiagrammen der Länder entnommen
Anteil der 15-Jährigen aus dem Anteil der 15- bis 19-Jährigen bestimmt
(D2) 15-Jährige in Ägypten über den Befehl: =C2*0,2
(E2) Damit 10- bis 15-Jährige in Ägypten über den Befehl: =B2+D2
alle weiteren Länder analog
(E12) Arithmetischer Mittelwert über den Befehl: =MITTELWERT(E2:E9)

Anteil der 0- bis 4-Jährigen und 5- bis 9-Jährigen aus den Bevölkerungsdiagrammen der Länder entnommen
(C2) 4-Jährige in Ägypten über den Befehl: =B2*0,2
(E2) Damit 4- bis 9-Jährige in Ägypten über den Befehl: =C2+D2
Migrantenzahl in RLP (2020) aus vorherigen Berechnungen bekannt
(G2) Ägyptische Kinder zwischen 4 und 9 Jahren in RLP über den Befehl: =RUNDEN(E2*F2;0)
alle weiteren Länder analog
(G12) Summe aller migrierten 4- bis 9-Jährigen in RLP (2020) über den Befehl: =SUMME(G2:G9)

Software: wxMaxima

Zur Bestimmung der Funktionswerte

Resultate der Modellierung

Im Jahr 2026 sind 214.079 Schüler in der Sekundarstufe 1.

Lehrerbedarf?

Zahl der Schüler nimmt bis 2026 zu
Zahl der Mathematiklehrkräfte nimmt ab
Bildung des Verhältnis Schüler pro Mathematiklehrer
Eine Lehrperson muss im Jahr 2026 mehr Schüler betreuen als im Jahr 2022
mögliche Folge: Qualitätsverlust im Mathematikunterricht
Bildungspolitiker sollten daher handeln

Bewertung und Optimierung

Kritik: Sättigungsgrenze $S$ als geschätzter Wert ungenau

→ Optimierung: Die Konstante

S

wird durch

S_{t}

ersetzt

Also:

f (t) = \frac{f (0) \cdot S}{f (0) + (S - f (0)) \cdot e^{- S \cdot k \cdot t}}

⇒

f (t) = \frac{f (0) \cdot S_{t}}{f (0) + (S_{t} - f (0)) \cdot e^{- S_{t} \cdot k \cdot t}}

$f (t) = \frac{f (0) \cdot S_{t}}{f (0) + (S_{t} - f (0)) \cdot e^{- S_{t} \cdot k \cdot t}}$

Dabei ist

S_{t} = E W_{t} \cdot M D_{t} \cdot M R P_{t}

$E W_{t}$ : Zahl der Einwohner in den Herkunftsländern zum Zeitpunkt $t$ (in diesem Zyklus: 310.416.000)
$M D_{t}$ : Anteil der Migranten, die zum Zeitpunkt $t$ nach Deutschland wandern (in diesem Zyklus: 20%)
$M R P_{t}$ : Anteil der Migranten, die zum Zeitpunkt $t$ nach Rheinland-Pfalz wandern (in diesem Zyklus: 5%)

Einwohnerzahlen sind keine statischen Größen
Anteile der Migranten, die nach Deutschland $M D_{t}$ oder Rheinland-Pfalz $M R P_{t}$ wandern, sind ebenfalls nicht konstant
Schwankungen durch Faktoren wie Klimawandel, Naturkatastrophen, politischer Lage oder Krieg

Es wurden folgende Aspekte nicht berücksichtigt:

Kinder, die in Rheinland-Pfalz geboren sind und vor Eintritt in die Sekundarstufe abwandern (z.B. in andere Bundesländer)
Kinder und ältere Menschen migrieren deutlich weniger

→ repräsentativ werden die Zahlen der Bevölkerungspyramide für die Altersstruktur genommen, obwohl das nicht der Altersstruktur der Migranten entspricht

Gewichtung des Mittelwertes (arithmetisches Mittel verwendet)
Migranten aus verschiedenen Herkunftsländern können sich unterschiedlich auf die Bundesländer verteilen

Literatur/Quellennachweise

↑ https://de.wikipedia.org/wiki/Liste_der_L%C3%A4nder_nach_Kindersterblichkeitsrate (Stand: 03.02.2022)
↑ https://de.statista.com/statistik/daten/studie/1221/umfrage/anzahl-der-auslaender-in-deutschland-nach-herkunftsland/ (Stand: 03.02.2022)
↑ https://www.statistik.rlp.de/fileadmin/dokumente/nach_themen/bev/kurz/Migration_Stand_15_05_17.pdf (Stand: 03.02.2022)
↑ https://www.populationpyramid.net/ (Stand: 31.01.2022)

Siehe auch

Wiki2Reveal

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung/Lehrerbedarf' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische%20Modellbildung/Lehrerbedarf/Modellierungszyklus%203
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

[1] ttps://de.wikipedia.org/wiki/Liste_der_L%C3%A4nder_nach_Kindersterblichkeitsrate (Stand: 03.02.2022)

[2] ttps://de.statista.com/statistik/daten/studie/1221/umfrage/anzahl-der-auslaender-in-deutschland-nach-herkunftsland/ (Stand: 03.02.2022)

[3] ttps://www.statistik.rlp.de/fileadmin/dokumente/nach_themen/bev/kurz/Migration_Stand_15_05_17.pdf (Stand: 03.02.2022)

[4] ttps://www.populationpyramid.net/ (Stand: 31.01.2022)

[1]

[2]

[3]

[4]

Kurs:Mathematische Modellbildung/Lehrerbedarf/Modellierungszyklus 3

Inhaltsverzeichnis

Einführung

Inhaltliche Beschreibung

Schülerzahl

Migration

Mathematisches Modell

Geburtenzahlen 2011-2016

Migration zwischen 2020 und 2026

Lineare Regression

Logistisches Wachstum

Bestimmung der Sättigungsgrenze S

Bestimmung der Wachstumskonstante k

Kinder zwischen 10 und 15 Jahren

Migration bis 2020

Zwischenfazit

Vergleich 2022

Geburtenzahlen 2007-2012

Software: Tabellenkalkulation

Software: wxMaxima

Resultate der Modellierung

Lehrerbedarf?

Bewertung und Optimierung

Literatur/Quellennachweise

Siehe auch

Seiteninformation

Wiki2Reveal

Navigationsmenü

Kurs:Mathematische Modellbildung/Lehrerbedarf/Modellierungszyklus 3

Einführung

Inhaltliche Beschreibung

Schülerzahl

Migration

Mathematisches Modell

Geburtenzahlen 2011-2016

Migration zwischen 2020 und 2026

Lineare Regression

Logistisches Wachstum

Bestimmung der Sättigungsgrenze S

Bestimmung der Wachstumskonstante k

Kinder zwischen 10 und 15 Jahren

Migration bis 2020

Zwischenfazit

Vergleich 2022

Geburtenzahlen 2007-2012

Software: Tabellenkalkulation

Software: wxMaxima

Resultate der Modellierung

Lehrerbedarf?

Bewertung und Optimierung

Literatur/Quellennachweise

Siehe auch

Seiteninformation

Wiki2Reveal

Navigationsmenü

Suche