Kurs:Mathematische Modellbildung/Lehrerbedarf/Implementation

Modellierungszyklus 1

Vorteile

• Open Source (LibreOffice)
• Einfache Programmierung von Makros
• Einfache deskriptive Statistik

Vorteile für die Schule

• Einfache Berechnungen
• Erstellung von Wertetabellen und Diagrammen
• Stochastische Experimente
• Numerische Verfahren

Implementation in Excel

• (C2) Anzahl Studienanfänger 2017 über: =RUNDEN(B2*0,6;0)
• (D7) Anzahl Absolventen 2022 über: =RUNDEN(C2*0,6;0)
• (E7) Anzahl fertig ausgebildeter Lehrkräfte 2022 über: =D7+10

Anwendungen (Beispiele)

• Numerische Verfahren, z.B. Newton Verfahren
• Monte-Carlo Simulation
• Mittelwert-, Varianzberechnung
• Wenn-Abfrage
• Zufallszahl
• Matrizenrechnung

Vorteile

• Dynamische Geometrie Software
• Open Source
• Für alle gängige Betriebssysteme
• Konstruktionswerkzeug mit Makros
• Präzise/sauber/genau
• Messfunktion

Vorteile für die Schule

• Erforschungswerkzeug
• Visualisierungswerkzeug
• Erstellung von digitalen Arbeitsblättern und Lernpfaden
• Automatische Konstruktionsbeschreibungen
• Figuren dynamisch verändern

Studienanfänger

• bessere Visualisierung
• Anzahl Studienanfänger (Y-Wert) abhängig vom Jahr (X-Wert) als Punkte $P_1,...,P_5$ eintragen
• Funktion interpolieren

Tabelle erstellen

• Ansicht, Tabelle

Tabelle ausfüllen

• A= Jahreszahlen
• B= Studentenanzahl

Punkte erstellen

• Werte in Tabelle markieren
• laues Balkensymbol auswählen
• Analyse zweier Variablen

Regressionsmodell

• wähle Sinus
• Sinusfunktion besseres "Werkzeug" als Polynomfunktion
• Sinus oszilliert zwischen oberer und unterer Schranke

• entstandene Funktionsgleichung:

$f(x)=41.9239\cdot sin(1.1956\cdot x+2.1237)+336.1706$

• Punkte liegen nicht direkt auf dem Graphen von $f$.
• neue Punkte $A,...,E$ erstellen, die dieselben $x$-Werte wie die Punkte $P_1,...,P_5$ haben, aber auf dem Graphen von $f$ liegen.
• $y$-Werte verändern sich geringfügig. Diese Änderung ist jedoch im Hinblick auf das Ziel der Modellierung vertretbar.

Implementation der Studienanfänger in GeoGebra

Stauchen des Graphens - Abbrecherquote

• Parameter einfügen
• $g(x)=a\cdot (41.9239\cdot sin(1.1956\cdot (x-c)+2.1237)+336.1706)+b$
• Parameter $a$ sorgt für Streckung bzw. Stauchung in y-Richtung
• hier $a$ $=0,6$(da Abbrecherquote 40% ⇒ 60% schließen Studium ab)

Implementation der Abbrecherquote in GeoGebra

Verschieben des Graphens in x-Richtung - Anzahl Absolventen

• Studiendauer: 5 Jahre
• Studienanfänger eines Jahres t sind Absolventen des Jahres t+5
• Graph von g um 5 Einheiten nach rechts verschieben durch Parameter c
• $g(x)=a\cdot (41.9239\cdot sin(1.1956\cdot (x-c)+2.1237)+336.1706)+b$

Implementation der Absolventen in GeoGebra

Verschieben des Graphens in y-Richtung - Quereinsteiger

• 10 Quereinsteiger jährlich
• g um 10 Einheiten nach oben verschieben durch Parameter b
• $g(x)=a\cdot (41.9239\cdot sin(1.1956\cdot (x-c)+2.1237)+336.1706)+b$

Implementation der Quereinsteiger in GeoGebra

Anwendungen (Beispiele)

• Hypothesentests
• Deskriptive Statistik
• Über Tool CAS: Ableitungen, Integrale, LGS lösen etc.
• Graphische Darstellungen
• Geometrische Konstruktionen

Modellierungszyklus 2

wxMaxima

Vorteile

• Open Source
• Benutzerfreundliche Oberfläche
• Einfache Bedienung
• Es gibt auch Maxima Web (und Maxima Konsole)

Allgemeines

• Computer Algebra System
• Eingabezeile gekennzeichnet durch %i(Nummer)
• Ausgabe gekennzeichnet durch %o(Nummer)
• Anweisungen mit Semikolon oder $-Zeichen abgeschlossen (wird selbstständig ergänzt)
• Bestätigung der Eingabe mit Shift & Return
• Dezimalzahlen mit Punkten statt mit Kommata eingeben

Teil 1

Im ersten Teil wird nur die durchgeführte Rechnung in Maxima beschrieben. In Teil 2 wird explizit auf die Implementierung in die Software eingangen.

• Um eine Vorhersage über die Anzahl an Absolventen nach einem Wanderungszyklus zu treffen, muss die Übergangsmatrix $W$ mit dem Vektor $A$ multipliziert werden
• Vektor $A$ gibt die aktuellen Absolventenzahlen plus Quereinsteiger (im Jahr 2022) vor der Wanderung an.

Das Ergebnis der Multiplikation der Übergangsmatrix $W$ mit dem Vektor $A$ wird dabei wieder als Vektor verstanden, der die Anzahl der Absolventen nach ihrer Wanderung angibt

• Der entstandene Vektor beinhaltet die Absolventen- und Quereinsteigerzahlen aus dem Jahr 2022 für die jeweiligen Bundesländer
• Die obige Rechnung wird nun weitere vier mal durchgeführt
• Die erste Zeile der Vektoren (Wert für RLP) wird für die Jahre 2023, 2024, 2025 und 2026 angepasst

Über "Algebra" auf "Matrix eingeben" klicken

Über "Algebra" auf "Matrix eingeben" klicken

Zeilen- und Spaltenanzahl der Matrix eingeben und diese benennen

Zeilen- und Spaltenanzahl der Matrix eingeben und diese benennen

Entsprechende Werte in die Matrix eintragen

Entsprechende Werte in die Matrix eintragen

2.Variante

Direkte Eingabe: Matrix wird zeilenweise eingegeben

• matrix([0.991,0.025,0.12],[0.009,0.945,0.28],[0,0.03,0.6])

• Analog zu Teil 1 wird die Übergangsmatrix $D$ mit dem Vektor $X$ multipliziert
• Dieser Vektor gibt dabei die Gesamtzahlen an pensionierten Lehrkräften, Lehrern im Dienst und Lehrern, die aufgrund gesundheitlicher Probleme pausieren, an (speziell für Mathematik in Rheinland-Pfalz)

Matrizenmultiplikation

Befehl zur Matrizenmultiplikation

Befehl zur Matrizenmultiplikation

Addition zweier Matrizen

Befehl zur Addition zweier Matrizen/Zahlen

Befehl zur Addition (zweier Matrizen)

Runden

Befehl zum Runden (eines Vektors)

Befehl zum Runden (eines Vektors)

• Nach der Multiplikation erhält man die entsprechenden Werte für ein Jahr später
• Da nicht nur Lehrer aus dem Dienst ausscheiden, werden im nächsten Schritt die neu eingestellten Lehrkräfte aus Teil 1 miteinbezogen und hinzu addiert
• Um Dezimalstellen zu vermeiden wird das Ergebnis zum Schluss noch gerundet

Die eben beschriebene Rechnung wird insgesamt fünf Mal (bis 2026), wobei der Startvektor die Zahlen aus dem Vorjahr enthält

Anwendungen (Beispiele)

• Matrizenrechnung (Inverse, Determinante etc.)
• Lösen von Gleichungen
• Bestimmung von Grenzwerten
• Integration
• Manipulation algebraischer Ausdrücke
• Faktorisieren von Polynomen
• Lösen von Differentialgleichungen erster/zweiter Ordnung

Modellierungszyklus 3

Vorteile

• Open Source (LibreOffice)
• Einfache Programmierung von Makros
• Einfache deskriptive Statistik

Vorteile für die Schule

• Einfache Berechnungen
• Erstellung von Wertetabellen und Diagrammen
• Stochastische Experimente
• Numerische Verfahren

Implementation der Migranten 2018 & 2020 in Excel

Implementation der Migranten 2018 & 2020 in Excel

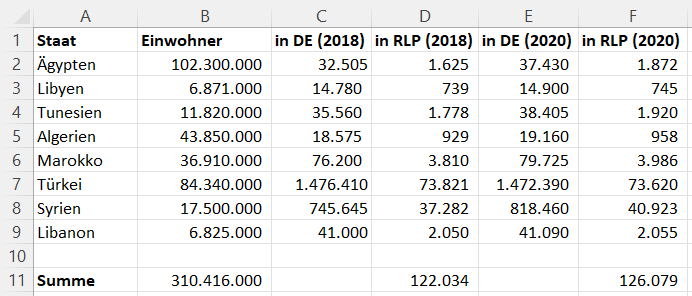
• Einwohnerzahl der Herkunftsländer und Migrantenzahl in Deutschland bekannt
• Migrantenzahl in Rheinland-Pfalz soll bestimmt werden
• (D2) Befehl für die Migranten aus Ägypten in RLP (2018): =RUNDEN(0,05*C2;0)
• (F2) Befehl für die Migranten aus Ägypten in RLP (2020): =RUNDEN(0,05*E2;0)
• alle weiteren Länder analog
• (D11), (F11) Summe der in Rheinland-Pfalz lebenden Migranten über den Befehl: =SUMME(D2:D9) bzw. =SUMME(F2:F9)

Implementation Anteile der Migranten in Excel

Implementation Anteile der Migranten in Excel

• Anteil der 10- bis 14-Jährigen und 15- bis 19-Jährigen aus den Bevölkerungsdiagrammen der Länder entnommen
• Anteil der 15-Jährigen aus dem Anteil der 15- bis 19-Jährigen bestimmt
• (D2) 15-Jährige in Ägypten über den Befehl: =C2*0,2
• (E2) Damit 10- bis 15-Jährige in Ägypten über den Befehl: =B2+D2
• alle weiteren Länder analog
• (E12) Arithmetischer Mittelwert über den Befehl: =MITTELWERT(E2:E9)

Implementation der Migrantenanteile bis 2020 in Excel

Implementation der Migrantenanteile bis 2020 in Excel

• Anteil der 0- bis 4-Jährigen und 5- bis 9-Jährigen aus den Bevölkerungsdiagrammen der Länder entnommen
• (C2) 4-Jährige in Ägypten über den Befehl: =B2*0,2
• (E2) Damit 4- bis 9-Jährige in Ägypten über den Befehl: =C2+D2
• Migrantenzahl in RLP (2020) aus vorherigen Berechnungen bekannt
• (G2) Ägyptische Kinder zwischen 4 und 9 Jahren in RLP über den Befehl: =RUNDEN(E2*F2;0)
• alle weiteren Länder analog
• (G12) Summe aller migrierten 4- bis 9-Jährigen in RLP (2020) über den Befehl: =SUMME(G2:G9)

Anwendungen (Beispiele)

• Numerische Verfahren, z.B. Newton Verfahren
• Monte-Carlo Simulation
• Mittelwert-, Varianzberechnung
• Wenn-Abfrage
• Zufallszahl
• Matrizenrechnung

wxMaxima

Vorteile

• Open Source
• Benutzerfreundliche Oberfläche
• Einfache Bedienung
• Es gibt auch Maxima Web (und Maxima Konsole)

Allgemeines

• Computer Algebra System
• Eingabezeile gekennzeichnet durch %i(Nummer)
• Ausgabe gekennzeichnet durch %o(Nummer)
• Anweisungen mit Semikolon oder $-Zeichen abgeschlossen (wird selbstständig ergänzt)
• Bestätigung der Eingabe mit Shift & Return
• Dezimalzahlen mit Punkten statt mit Kommata eingeben

• Funktionen definieren über ":="
• %e für die Eulersche Zahl
• Verwendung von Punkten bei Dezimalzahlen

Maxima 3.Zyklus Funktionswerte

Funktionen (Beispiele)

• Matrizenrechnung (Inverse, Determinante etc.)
• Lösen von Gleichungen
• Bestimmung von Grenzwerten
• Integration
• Manipulation algebraischer Ausdrücke
• Faktorisieren von Polynomen
• Lösen von Differentialgleichungen erster/zweiter Ordnung

Siehe auch

• Wiki2Reveal

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische%20Modellbildung/Lehrerbedarf/Implementation
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.